Эрик Роджерс - Физика для любознательных. Том 2. Наука о Земле и Вселенной. Молекулы и энергия

В современной механике эта задача представляет собой случай сохранения момента количества движения . Что такое момент количества движения [96] Эту величину у вращающегося вокруг своей оси тела мы называем моментом вращения или просто спином в случае электрона, но для планет, вращающихся вокруг Солнца, применяется общий термин — момент количества движения. Такой термин применяется как для тел, вращающихся вокруг своей оси, так и для тел, движущихся по орбите. и почему мы уверены, что он сохраняется? Ниже дано краткое объяснение, слишком примитивное, чтобы быть убедительным, но имеющее целью дать общее представление об этом фундаментальном законе сохранения.

Прямолинейное движение описывается такими понятиями, как расстояние (s), скорость (v), ускоряющая сила (F)…. законами и соотношениями типа F∙Δ t= Δ( Mv)…, и такими принципами, как сохранение количества движения. Когда тело вращается, не совершая поступательного движения, мы можем применить законы Ньютона к каждой его движущейся части и составить эквивалентную схему. Вместо пройденного расстояния мы будем теперь иметь угол поворота (выраженный в радианах или числе оборотов). Вместо линейной скорости мы будем иметь дело с угловой скоростью (в оборотах в минуту или в радианах в секунду). Вместо силы будет фигурировать момент силы , равный произведению силы на плечо , — причина, заставляющая тело вращаться все быстрее и быстрее. Соотношению

СИЛА∙ВРЕМЯ = ПРИРАЩЕНИЕ КОЛИЧЕСТВА ДВИЖЕНИЯ,

т. е. второму закону Ньютона, будет соответствовать

МОМЕНТ СИЛЫ∙ВРЕМЯ = ПРИРАЩЕНИЕ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ.

Задумайтесь над смыслом момента количества движения, и вы, вероятно, придете к правильному заключению: подобно тому как момент силы равен произведению силы на плечо ( F ∙ r ), момент количества движения равен количеству движения , умноженному на плечо ( Mv ∙ r ).

Умножьте F и Mv на плечо относительно выбранной оси, и вы получите вариант второго закона Ньютона для случая вращательного движения. Плечо — это перпендикуляр , проведенный от оси в направлении действия вектора силы или количества движения.

Предположим, что два невращающихся тела сталкиваются и в результате одно из них начинает вращаться. Силы взаимодействия тел равны и противоположно направлены (третий закон Ньютона); плечо относительно произвольной оси для этих сил будет одними тем же. Поэтому моменты силы обоих тел относительно выбранной нами оси будут одинаковы по величине и противоположны по направлению. Приобретенный одним телом при столкновении момент количества движения будет равен по величине моменту количества движения второго тела , а их направления будут противоположными. Следовательно, полный момент обоих тел, приобретенный ими в процессе столкновения, равен нулю. Если одно тело начинает вращаться, другое тоже будет вращаться, но в противоположную сторону, вокруг той же оси. При любом столкновении или другом виде взаимодействия момент количества движения сохраняется , он может только передаваться без потерь или могут возникать равные по величине и противоположные по направлению моменты количества движения.

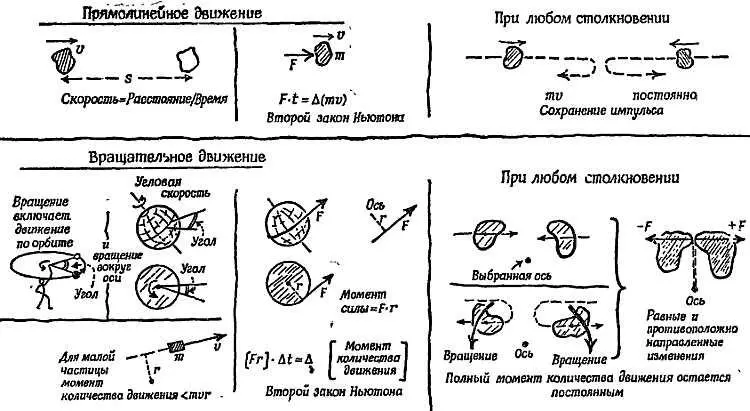
Фиг. 159. Вращения и столкновения.

Ввиду этого вращающееся изолированное тело (например, фигурист, вращающийся на одном коньке) не может изменить своего момента количества движения. Сумма произведений Mv ∙ r , относящихся к различным его частям, не может измениться. Предположим, что тело сжимается (фигурист сводит руки). Тогда величины r убывают для частей тела, приближающихся к оси вращения, и если полный момент остается постоянным, величина Mv должна возрасти — тело начнет вращаться быстрее . Понаблюдайте за фигуристом: независимо от его желания он вращается быстрее, если сводит руки или сгибает вытянутую ногу.

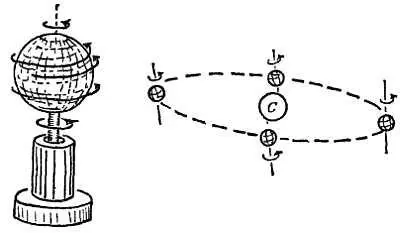
Фиг. 160. Момент количества движения вращающегося вокруг своей оси шара остается неизменным, если к нему не приложен момент внешней силы.

« Изолированное вращающееся тело не может изменить своего момента количества движения». Примените это положение к вращающейся Земле, к человеку на вращающемся без трения стуле. Превратитесь сами в «изолированное вращающееся тело»: начните вращаться, встав на одну пятку так, чтобы вы смогли повернуться несколько раз, прежде чем силы трения остановят ваше движение. (Еще лучше встать или сесть на табуретку, которая свободно вращается.) Возьмите тяжелую книгу и подержите ее на расстоянии вытянутой руки. Теперь, начав вращаться, прижмите книгу быстро к себе. Обратите внимание, как это отразится на вашей скорости. В этом случае момент количества движения сохраняется. Но здесь применим и второй закон Кеплера: книга — «планета», притягиваемая вами — «Солнцем» — во время ее вращения. (В этом опыте участвует ваша масса, которая имеет большую величину, поэтому вы не сможете с достаточной точностью проверить закон Кеплера.)