Для реальной планеты притяжение Солнца не создает момента силы относительно оси, проходящей через Солнце, и, следовательно, не может изменить момент количества движения планеты относительно Солнца . На самом деле последний равен Mv ∙ r , где r — не «рычаг» Кеплера, а отрезок перпендикуляра , опущенного из центра Солнца на касательную к орбите (линию скорости). Когда планета приближается к Солнцу, r уменьшается и, чтобы Mvr было постоянным, v должна возрастать в той же самой пропорции.
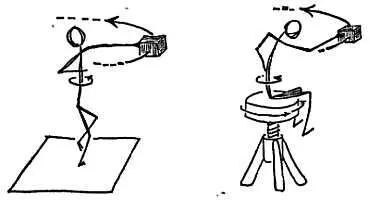
Фиг. 161. Человек на вращающейся площадке увеличивает скорость вращения, когда приближает груз к оси.
Предположим, что за очень короткое время t планета проходит небольшой участок орбиты s со скоростью v= s/ t. На этом участке момент количества движения планеты относительно Солнца равен Mr ∙( s / t ), или Ms ∙ r / t . Но s ∙ r равно произведению высоты на основание малого треугольника , который за время t описывает радиус-вектор. Эта величина равна удвоенной площади треугольника!
Следовательно,
МОМЕНТ КОЛИЧЕСТВА ДВИЖЕНИЯ ПЛАНЕТЫ = (МАССА М)∙(ДВОЙНАЯ ПЛОЩАДЬ, ОПИСЫВАЕМАЯ РАДИУСОМ-ВЕКТОРОМ) / ВРЕМЯ t
Для случая притяжения Солнцем отношение
ОПИСЫВАЕМАЯ ПЛОЩАДЬ/ВРЕМЯ
не меняется: согласно второму закону Кеплера, величина описываемой в единицу времени радиусом-вектором площади не может измениться. Следовательно, когда Кеплер открыл свой второй закон, он показал лишь, что сила притяжения планет направлена точно к Солнцу и что не существует других сил, таких, как трение, обусловленное вязким эфиром.
Закон сохранения момента количества движения столь же универсален, как и другие законы сохранения механики — сохранение массы, количества движения и т. д. В атомной физике мы называем его сокращенно законом сохранения спина и не сомневаемся в его справедливости даже в сложнейших взаимодействиях между частицами и излучением.
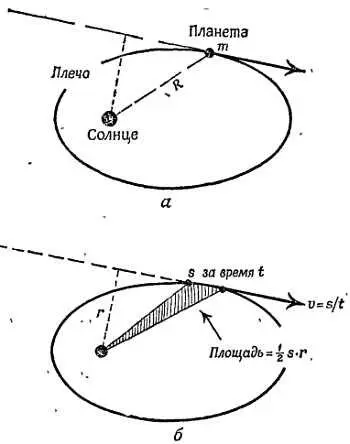
Фиг. 162. Момент количества движения планеты mvr= m∙( s/ t)∙ r= m∙( двойная площадь)/ время.
Плодотворная теория
Ньютон создавал свою теорию последовательно: сформулировал законы движения как исходные пункты разумных предположений, подкрепленных соображениями, полученными из экспериментальных данных; затем получил следствия законов, такие, как законы Кеплера, а затем проверил эти выводы на опыте. В случае законов Кеплера эксперименты уже были сделаны. Наблюдения Тихо Браге были прекрасной проверкой, так что, когда Ньютон получил теоретические результаты, экспериментальная проверка теории уже была заранее готова. Не приходилось поэтому сомневаться в том, что теория «верна». Теория оказалась ценнее отдельных фактов. Она давала ясное и полное представление о движении планет, связывая его с таким привычным явлением, как падение тел. Вооруженный мощными математическими методами и руководимый великолепной интуицией, Ньютон применил свою теорию к большому числу задач, вошедших в его Принципы. Некоторые из этих задач рассмотрены ниже.
I. Определение массы Солнца и Земли
Ньютон вычислил массу Солнца, выразив ее в земных массах. [В то время масса Земли не была известна и не могла быть определена без измерений, подобных более поздним измерениям, проведенным Кавендишем (см. гл. 23 )
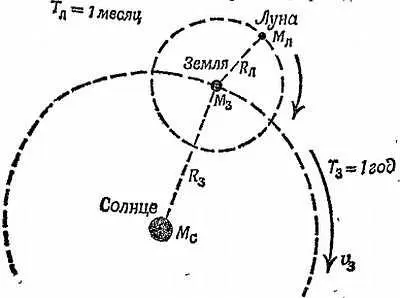
Фиг. 163. Вычисление отношения массы Солнца к массе Земли.
Вычисления могут быть выполнены следующим путем. (Индексы С, 3 и Л относятся к Солнцу, Земле и Луне соответственно.)
Для Движения Земли по орбите вокруг Солнца.
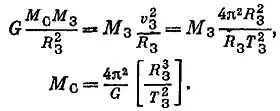
Обратите внимание, что масса Земли М Зсократилась,
Для движения Луны по орбите вокруг Земли:
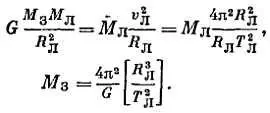
Вновь масса Луны М Лсократилась Теперь, разделив одно уравнение на другое, получим
Читать дальше




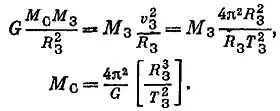
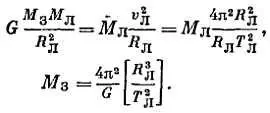







![Йэн Стюарт - Математика космоса [Как современная наука расшифровывает Вселенную]](/books/429584/jen-styuart-matematika-kosmosa-kak-sovremennaya-nau-thumb.webp)



