Эрик Роджерс - Физика для любознательных. Том 2. Наука о Земле и Вселенной. Молекулы и энергия

R 3/ T 2= G∙ M/4π 2

Если перейти теперь к другой планете, с другим радиусом орбиты R ' и периодом обращения Т ', то новое отношение ( R ') 3/( T ') 2будет опять равно G ∙ M /4π 2; эта величина будет одинаковой для всех планет , так как G — универсальная постоянная, а масса М — одна и та же для всех планет, вращающихся вокруг Солнца. Таким образом, величина R 3/ T 2будет одной и той же для всех планет в согласии с третьим законом Кеплера. Для других систем, например для спутников Юпитера, величина М будет другой (в этом случае М — масса Юпитера), a R 3/ T 2будет иметь другое значение, одинаковое для всех спутников.

Масса планеты m сокращается. Несколько планет с различными массами могли выдвигаться по одной и той же орбите. Вы могли бы об этом догадаться — ведь это знаменитый эксперимент, но в космическом масштабе.

Если закон убывания силы тяжести отличается от закона обратных квадратов, то отношение R 3/ T 2не будет одним и тем же для всех планет. Например, если использовать закон обратной пропорциональности кубу расстояния, то для всех планет постоянной будет величина R 4/ T 2; в этом случае величины R 3/ T 2будут пропорциональны 1/ R и для разных планет будут разными. В действительности, как установил Кеплер, эти величины одни и те же. Это означает, что справедлив закон обратных квадратов.

Дифференциальное исчисление позволяет получить третий закон и для эллиптических орбит, но в этом случае R — средняя величина между наибольшим и наименьшим расстоянием планеты от Солнца.

Второй закон Кеплера

Приведем приближенные вычисления, выполненные Ньютоном. Будем основываться на втором законе Ньютона: изменение количества движения равно F ∙Δ t . Следовательно, изменение mv — вектор, направленный по линии действия силы F и пропорциональный ее величине.

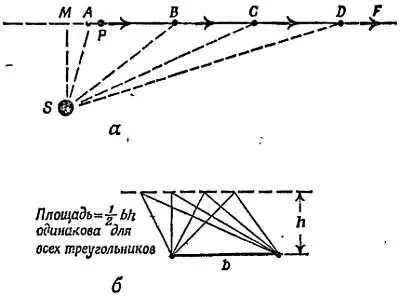
Фиг. 153. Свободное движение планеты.

а— планета Р движется прямолинейно о постоянной скоростью, за равные промежутки времени радиус-вектор описывает равные площади; б— свойства треугольников, которыми мы здесь пользуемся.

Вначале предположим, что планета движется свободно, т. е. на нее не действуют силы. Мы можем провести радиусы, соединяющие планету с Солнцем, лишенным гравитации (фиг. 153). Планета Р будет двигаться с постоянной скоростью по прямой линии AF (первый закон Ньютона). Обозначим расстояния, пройденные планетой за одинаковые интервалы времени: АВ, ВС, CD и т. д. Так как скорость постоянна, то AB = BC = CD и т. д.

Рассмотрим площади, описываемые радиусом SP в процессе движения. Как сравнить треугольники SAB, SBC, SCD ? У всех этих треугольников одинаковые высоты SM и одинаковые основания АВ, ВС, CD . Из этого следует, что площади треугольников равны. Радиус-вектор, проведенный из точки S , описывает одинаковые площади за равные интервалы времени, так что это простое движение подчиняется закону Кеплера.

Теперь предположим, что планета движется по орбите благодаря тому, что Солнце притягивает ее и сила притяжения направлена по радиусу PS . Чтобы упростить геометрическое рассмотрение, предположим, что притяжение действует только в точках А, В, С …. траектории, а остальное время планета движется свободно по прямой линии. Тогда траектория планеты будет выглядеть так, как показано на фиг. 154.

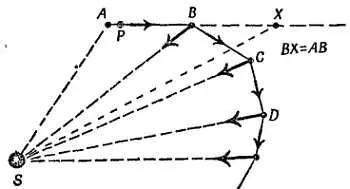
Фиг. 154. Движение планеты с «импульсным» притяжением.

В отсутствие притяжения в точке В планета Р двигалась бы по оси X .

Предположим, что планета проходит отрезки АВ, ВС, CD и т. д. за одинаковые отрезки времени, а внешнее усилие возникает только в точках В, С, D и т. д. Планета движется равномерно вдоль АВ , затем в точке В испытывает мгновенное воздействие по направлению BS и резко изменяет свою скорость, начиная двигаться (уже с другой скоростью) вдоль ВС . Если исключить из рассмотрения точку В , то планета будет продолжать двигаться прямолинейно, как в рассмотренном выше простом примере! Продолжив прямую линию, отложим на ней отрезок ВХ , равный АВ . Если не учитывать притяжения в точке В , то планета пройдет расстояния АВ и ВХ за одинаковые отрезки времени, и радиус-вектор, проведенный из точки X , опишет одинаковые треугольники SAB и SBX . Но в действительности планета достигает вместо точки X положения С .