Эрик Роджерс - Физика для любознательных. Том 2. Наука о Земле и Вселенной. Молекулы и энергия

И вот, наконец, Ньютону удалось объяснить, откуда берется эта сила. Он предположил, что силы, заставляющие падать тела на поверхность Земли, могут также притягивать Луну и служат причиной ее движения по орбите. Существует легенда о том, что Ньютон обдумывал эту проблему, сидя в саду, и яблоко, упавшее ему на голову, подсказало решение. Такое притяжение мы называем «гравитацией» — словом, которое означает тяжесть или подразумевает какую-то связь с весом. Во многих случаях более подходит обычное слово вес.

Фиг. 148. Земное притяжение.

Ньютон предположил, что именно вес Луны удерживает ее на орбите. Если бы Луна находилась очень близко от поверхности Земли, то ее вес обусловливал бы ее ускорение g , равное примерно 9,81 м/сек 2, т. е. такое же, как и у яблока, если не считать, что объем Луны больше, и это, конечно, не разрешает поставить подобный эксперимент. Будет ли Луна иметь такое же ускорение на своей орбите? Будет лила орбите Луны v 2/ R ~ 9,81 м/сек 2?Луна совершает полный оборот по своей орбите относительно неподвижных звезд за 27,3 дня. Ньютон знал, что радиус лунной орбиты R равен 60 радиусам земного шара, т. е. 60 R . Ему был также приближенно известен радиус Земли, так что он мог вычислить скорость v , разделив длину окружности лунной орбиты 2π R на время Т , равное одному месяцу, а отсюда вычислялось ускорение v 2/ R . В ответе получалась величина, значительно меньшая 9,81 м/сек 2. Если «гравитация» меняется с расстоянием, g может быть значительно меньше на лунной орбите. Ньютон нашел простое правило убывания силы притяжения — закон обратной пропорциональности квадрату расстояния. По закону обратных квадратов убывают с расстоянием сила света, интенсивность радиоволн, звука, а также сила, создаваемая магнитным полюсом или электрическим зарядом.

Закон обратных квадратов справедлив во всех случаях прямолинейного распространения из источника при отсутствии поглощения [93] Предположим, что небольшой распылитель испускает струю мелких капель масла. Эти капли летят из ствола по прямым линиям, образуя широкий конус. Если экран (кусок хлеба, скажем) полностью перекрывает конус на расстоянии 1 м от ствола, то на расстоянии 2 м конус можно перекрыть экраном, площадь которого будет в 4 раза больше, а на расстоянии в 3 м — в 9 раз больше первого, поэтому толщина масла на экранах будет в пропорция 1:1/4:1/9… Это — «закон обратных квадратов намазывания маслом». Фиг. 149. Закон, обратных квадратов. . Правильная мысль пришла в голову Ньютону, когда он пытался получить третий закон Кеплера! Он попробовал применить зависимость, обратно пропорциональную квадрату расстояния. Луна находится на расстоянии шестидесяти земных радиусов, а яблоко — на расстоянии лишь одного радиуса от центра Земли, поэтому притяжение в области Луны уменьшается в 1/60 2раз, или в 3600 раз. Ускорение Луны уже будет не 9,81 м/сек 2, а 9,81/3600 м/сек 2. Легко подсчитать значение v 2/ R для Луны и убедиться, что оно совпадает с «предсказанной» таким способом величиной. Представьте себе тот восторг, который вы бы испытали, открыв это соответствие! Это была успешная проверка соотношений F= M∙ aи a= v 2/ Rи закона обратных квадратов для силы тяжести. Вы могли бы сделать первую проверку выдающейся теории — и великое открытие принадлежало бы вам!

Однако сам Ньютон, полный нетерпения, но дальновидный, не был полностью удовлетворен этой проверкой. По непостижимым причинам он отложил все вычисления еще на несколько лет. По-видимому, он стремился решить задачу о притяжении тела шаром с распределенной равномерно в нем массой, подобным Земле. Он уменьшил величину g в 60 2раз, но уменьшение от 1 до (1/60) 2предполагает, что тело на поверхности Земли, для которого ускорение g = 9,81 м/сек 2, находится как бы на расстоянии одного земного радиуса от притягивающего центра. Притягивает ли громадный круглый земной шар яблоко так, как если бы вся масса Земли была сосредоточена в ее центре на расстоянии 6300 км от поверхности? Близкие от яблока части земной массы должны притягивать его очень сильно (согласно закону обратных квадратов).

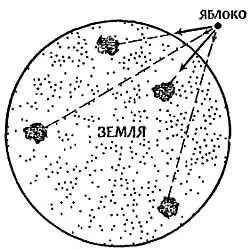
Фиг. 150.Задача Ньютона.

Яблоко, притягиваемое различными частями Земли (показаны четыре отдельных элемента)