Эрик Роджерс - Физика для любознательных. Том 2. Наука о Земле и Вселенной. Молекулы и энергия

Где G — универсальная постоянная; М 1и М 2— массы; d — расстояние между ними; F — сила, с которой каждое тело притягивает другое. Нужно помнить, что универсальная постоянная G имеет другой физический смысл, нежели g , — локальное значение ускорения силы тяжести [95] Для случая Земли и яблока М 1 и М 2 — соответственно массы Земли и яблока; расстояние между ними равно радиусу Земли r . Таким образом, вес яблока M 2 g = GM 1 M 2 / r 2 . Отсюда следует связь между g и G : g = G ∙ M 1 / r 2 УСКОРЕНИЕ g = ГРАВИТАЦИОННАЯ ПОСТОЯННАЯ ∙ МАССА ЗЕМЛИ / (РАДИУС ЗЕМЛИ) 2 .

Могут ли эти общие законы объяснить движение планет? Ньютон доказал, что могут. Он показал, что притяжение по выведенным им законам обусловливает движение планет по эллиптическим орбитам, причем в одном из фокусов эллипса должно находиться Солнце. Ему удалось легко вывести два других закона Кеплера, которые также вытекают из его гипотезы всемирного тяготения. (Эти законы справедливы, если учитывается только притяжение Солнцем. Но мы должны учитывать и действие на движущуюся планету других планет.) В Солнечной системе эти притяжения незначительны по сравнению с притяжением Солнца, однако в точных расчетах ими нельзя пренебречь.

Так Ньютон перенес простое представление о движении Луны на всю планетную систему. Он предположил, что любое тело притягивается другим с силой, пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними. На основе этой гипотезы он создал подробную картину движения тел в Солнечной системе, свод законов, которые проверялись точными измерениями в течение двух столетий. Спутники планет подчиняются тем же законам. Даже кометы следуют общему правилу. И все эти движения определяются силой тяжести, которая хорошо известна на Земле. Ньютон объяснил небесную систему на основе единой рациональной схемы.

Это столь большое достижение, что следует специально проследить путь, которым Ньютон получил три закона Кеплера и затем использовал их в дальнейшей работе. Первое доказательство того, что движение планеты происходит по эллипсу, можно сделать либо используя изобретенное Ньютоном дифференциальное исчисление, либо опираясь на сложные и громоздкие геометрические доказательства. (Ньютон получил доказательство и геометрическим путем, чтобы убедить в своей правоте противников дифференциального исчисления.) Мы с большим сожалением опускаем это доказательство.

Выведем теперь третий закон Кеплера, а затем второй закон — закон равных площадей за равные времена. Второй закон следует из произвольной зависимости силы притяжения от расстояния, если эта сила действует по прямой, соединяющей центры планеты и Солнца. Но первому и третьему законам Кеплера удовлетворяет только закон обратной пропорциональности сил притяжения квадрату расстояния.

Третий закон Кеплера

Чтобы получить третий закон Кеплера, Ньютон просто объединил законы движения с законом всемирного тяготения. Эллиптические орбиты движения планеты получаются, если использовать методы дифференциального исчисления, учитывающего изменения радиуса и скорости планеты. В результате таких вычислений получится третий закон Кеплера.

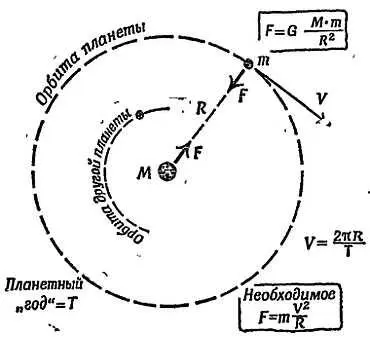
Фиг. 152. Движение планет.

Для случая круговых орбит можно рассуждать следующим образом: пусть планета, масса которой равна m , движется со скоростью v по окружности радиуса R вокруг Солнца, масса которого равна М . Это движение может осуществляться только в том случае, если на планету действует внешняя сила mv 2/ R , создающая центростремительное ускорение v 2/ R (см. гл. 21 ). Предположим, что притяжение между Солнцем и планетой как раз и создает необходимую силу. Тогда

G∙( M∙ m/ d 2) = m∙ v 2/ R

и расстояние d между m и М равно радиусу орбиты R . Но скорость

v= ДЛИНА ОКРУЖНОСТИ / ПЕРИОД ОБРАЩЕНИЯ = 2π R/ T

где Т — время, за которое планета совершает один оборот. Тогда

G∙( M∙ m/ R 2) = [(2π R/ T )2/ R]∙ m; G∙( M∙ m/ R 2) = 4π 2 m∙ R 2/ T 2 R

Чтобы получить третий закон Кеплера, нужно перенести все R и T в одну сторону уравнения, а все остальные величины — в другую: