Эрик Роджерс - Физика для любознательных. Том 2. Наука о Земле и Вселенной. Молекулы и энергия

Повлияет ли это на равенство площадей? Если планета приходит в точку С , то нужно рассматривать треугольники SAB и SBC . Равны ли эти треугольники? Усилие действует в точке В по направлению к Солнцу вдоль прямой линии BS и изменяет направление движения. Это усилие придает планете добавочное количество движения, направленное по прямой BS , которое, складываясь с ее начальным количеством движения, обеспечивает движение планеты по прямой ВС . Начальное количество движения направлено по прямой АВ . Поэтому

НАЧАЛЬНОЕ КОЛИЧЕСТВО ДВИЖЕНИЯ, НАПРАВЛЕННОЕ ПО АВ + ДОБАВОЧНОЕ КОЛИЧЕСТВО ДВИЖЕНИЯ, НАПРАВЛЕННОЕ ВДОЛЬ BS = НОВОЕ КОЛИЧЕСТВО ДВИЖЕНИЯ, НАПРАВЛЕННОЕ ПО ВС .

Из второго закона Ньютона следует, что количество движения по ВС — вектор. Поэтому суммирование необходимо проводить по законам векторного сложения (фиг. 155).

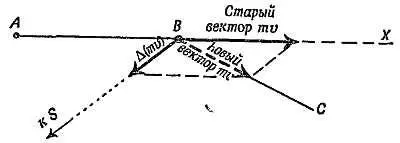
Фиг. 155. Изменение количества движения в точке В.

Так как масса планеты постоянна, то мы можем сократить ее и пользоваться для сложения скоростями:

СКОРОСТЬ ВДОЛЬ АВ+ ПРИРАЩЕНИЕ СКОРОСТИ ВДОЛЬ BS= СКОРОСТЬ ПО НАПРАВЛЕНИЮ ВС.

Изобразим скорость планеты вдоль прямой АВ отрезком АВ . Тогда отрезок ВХ также будет равен этой скорости, а отрезок ВС будет соответствовать новой скорости планеты, направленной по прямой ВС (так как все отрезки равны расстояниям, проходимым за равные промежутки времени). Пользуясь этим масштабом, мы можем построить векторную диаграмму (фиг. 156), выражающую записанные выше уравнения.

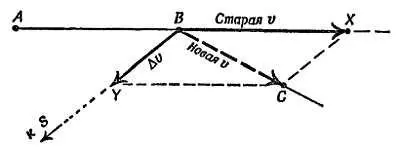
Фиг. 156. Повторение фиг. 165 для скоростей.

Масштаб выбран таким, чтобы АВ или ВХ равнялись начальной скорости вдоль АВ , до ее изменения под действием силы притяжения в точке В .

Пусть ВХ (= AВ ) — начальная скорость до воздействия усилия, а ВС — конечная скорость после воздействия. Изменение скорости будет равно вектору BY , направленному по линии BS в сторону точки S . Построив параллелограмм с диагональю ВС , получим требуемый результат. Из свойств параллелограмма следует, что сторона ХС параллельна BY , так что точка С лежит на линии, параллельной BS .

Теперь рассмотрим треугольники SBC и SBX , представленные на фиг. 157.

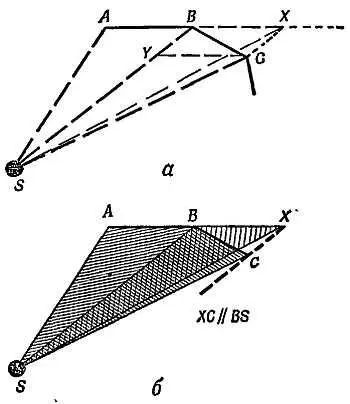
Фиг. 157. Повторение фиг. 154, точка Слежит на прямой ХС, параллельной BYили ВS( а); треугольники одинаковой площади заштрихованы ( б).

Они имеют одно и то же основание BS и находятся между параллельными прямыми, поэтому площади их равны. Площадь SBC равна площади SBX , которая в свою очередь равна площади SBА . Следовательно, треугольники SBА и SBC имеют одинаковую площадь. По аналогичным причинам треугольники SBC и SCD тоже имеют равные площади. В конечном итоге все площади треугольников равны между собой и закон Кеплера для этого движения выполняется. При этом необходимо, чтобы усилие всходило из одной и той же точки S . Если теперь чаще прикладывать усилие (но соответственно меньшее по величине), мы получим орбиту, как на фиг. 158, близкую к гладкой кривой. При этом будет соблюдаться и закон Кеплера, потому что сила направлена от планеты к Солнцу . Если прикладывать усилия еще чаще, то в пределе мы придем к случаю непрерывной силы с орбитой в виде гладкой кривой. Это и доказывает справедливость второго закона Кеплера для гладкой криволинейной орбиты.

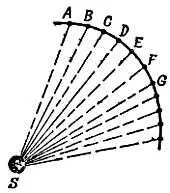
Фиг. 158. Уменьшение равных интервалов времени от Адо В, от Вдо С.

Орбита близка к гладкой кривой. Когда орбита представляет собой гладкую кривую, каждый сегмент, перекрываемый за равные времена, можно рассматривать как малый треугольник. Следовательно, у всех сегментов должна быть одинаковая площадь

Второй закон Кеплера и момент количества движения

Ньютон пришел ко второму закону Кеплера, исходя из основных положений своей механики. Закон обратных квадратов для этого не требуется. Любое притяжение, направленное к Солнцу как центру, будет обеспечивать выполнение этого закона.