Вадим Цудикман - Опционы - Разработка, оптимизация и тестирование торговых стратегий

На практике оба эти сценария встречаются крайне редко. Обычно капитал распределяется неким промежуточным образом, когда потенциально более привлекательные комбинации получают больше капитала, чем менее привлекательные. Привлекательность определяется с помощью специальных показателей, семь из которых были подробно рассмотрены в разделах 4.3.1 и 4.3.2. Портфели, в которых большая часть капитала распределена между несколькими комбинациями, мы будем называть «концентрированными». А портфели, в которых доля капитала, инвестированного в разные комбинации приблизительно одинакова, будем называть «равномерными».

Степень концентрированности капитала является важным показателем для сравнения между собой различных способов распределения капитала. Дело в том, что уровень диверсификации портфеля чрезвычайно важен для управления и контроля рисков. Ранее мы оценивали диверсификацию портфеля по количеству базовых активов, включенных в его состав (рис. 4.4.5). Однако, даже если портфель состоит из комбинаций, относящихся к большому количеству базовых активов, он может тем не менее быть слабо диверсифицированным, если большая часть капитала сконцентрирована в комбинациях, относящихся к одному (или нескольким) активам. Если же капитал распределен более-менее равномерно между комбинациями, относящимися к разным базовым активам, то такой портфель является более диверсифицированным и, соответственно, менее рискованным.

Ранее мы выражали степень концентрированности капитала путем расчета коэффициента вариации весов различных комбинаций, входящих в состав портфеля (раздел 4.3.2, таблица 4.3.2). Поскольку сейчас мы обрабатываем большой массив данных (6448 портфелей для каждого из семи показателей распределения капитала) целесообразно будет ввести другой, более удобный и статистически более обоснованный показатель. Назовем его «индекс концентрированности портфеля».

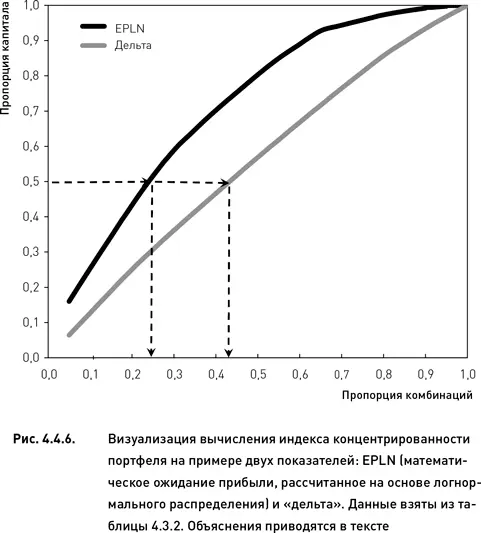
Продемонстрируем расчет индекса концентрированности на примере данных таблицы 4.3.2 и двух показателей, математического ожидания прибыли и дельты. На основе каждого из этих двух показателей был сформирован портфель, состоящий из 20 комбинаций. Данные портфели отличаются друг от друга только набором весов w , в соответствии с которыми распределяется капитал между комбинациями. Для каждого портфеля отсортируем все комбинации по весу инвестированного в них капитала. Рассчитаем кумулятивную пропорцию капитала для двух комбинаций с наибольшим весом, затем для трех комбинаций и так далее до 20-й комбинации. Построим функцию зависимости кумулятивной пропорции от пропорции комбинаций в портфеле (отношение числа комбинаций, для которых было рассчитано данное значение кумулятивной функции к общему количеству комбинаций в портфеле). Например, для портфеля, сформированного по показателю «математическое ожидание прибыли», три комбинации с наибольшими весами имеют суммарный вес 0,34 (значение функции кумулятивной пропорции). Соответствующее этому весу значение пропорции комбинаций в портфеле равно 3/20 = 0,15. Это означает, что 34 % капитала сосредоточено в 15 % комбинаций.

На рис. 4.4.6 показаны две функции кумулятивной пропорции, соответствующие показателям «математическое ожидание прибыли» и «дельта» (данные взяты из таблицы 4.3.2). Используя эти функции, можно рассчитать, в каком проценте комбинаций (от общего числа комбинаций в портфеле) сосредоточено 50 % капитала. Это и будет значением индекса концентрированности портфеля. Для показателя «математическое ожидание прибыли» индекс равен 0,25, а для дельты он равен приблизительно 0,42. Это означает, что при распределении капитала по матожиданию прибыли 50 % капитала оказалось вложенным в 25 % комбинаций, а при формировании портфеля по показателю дельты половина капитала была вложена в 42 % комбинаций. Следовательно, в данном примере использование показателя «математическое ожидание прибыли» приводит к более концентрированному распределению капитала и, соответственно, созданию менее диверсифицированного портфеля.

Используя эту методику, мы рассчитали значения индекса концентрированности для каждого из 6448 портфелей, сформированных на исследуемом историческом периоде с помощью одного из семи показателей. Для того чтобы сравнить степень концентрированности капитала при формировании портфеля с помощью разных показателей, мы построили частотное распределение индекса концентрированности для каждого отдельно взятого показателя (рис. 4.4.7).