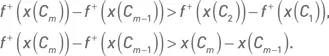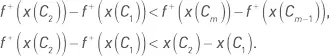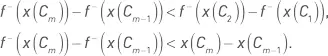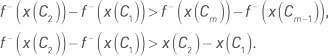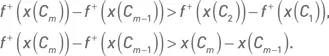
На низких интервалах значений исходной функции приращение значений выпуклой функции меньше, чем на высоких интервалах значений. Разница в значениях трансформированной функции между комбинацией со вторым по величине значением показателя и комбинацией с первым (самым низким) значением показателя меньше, чем разница в значениях трансформированной функции между комбинацией со средним или высоким значением показателя и комбинацией с предыдущим значением показателя. Кроме того, на низких интервалах значений исходной функции приращение значений выпуклой функции меньше, чем приращение значений самой исходной функции. Формально это можно выразить следующими неравенствами:
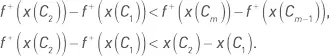
На высоких интервалах значений исходной функции приращение значений вогнутой функции меньше, чем на низких интервалах значений исходной функции. Другими словами, разница в значениях трансформированной функции между комбинацией с наибольшим значением показателя и комбинацией со вторым по величине значением показателя меньше, чем разница в значениях трансформированной функции между комбинацией со средним или низким значением показателя и комбинацией с предыдущим значением показателя. Кроме того, на высоких интервалах значений исходной функции приращение значений вогнутой функции меньше, чем приращение значений самой исходной функции. Формально это можно выразить следующим образом:
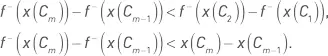
На низких интервалах значений исходной функции приращение значений вогнутой функции больше, чем на высоких интервалах значений. Разница в значениях трансформированной функции между комбинацией со вторым по величине значением показателя и комбинацией с первым (самым низким) значением показателя больше, чем разница в значениях трансформированной функции между комбинацией со средним или высоким значением показателя и комбинацией с предыдущим значением показателя. Кроме того, на низких интервалах значений исходной функции приращение значений вогнутой функции больше, чем приращение значений самой исходной функции. Формально это можно выразить следующими неравенствами:
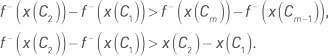
Расчет весов по трансформированным весовым функциям
В тот момент, когда все значения трансформированной функции определены, расчет весов производится по формуле 4.3.5. Правый график рис. 4.4.8 показывает веса, рассчитанные по весовым функциям, представленным на левом графике этого рисунка (данные взяты из таблицы 4.3.2; исходная весовая функция – показатель «математическое ожидание прибыли»; выпуклая и вогнутая функции рассчитаны по формуле 4.4.1 при n = 2 и n = 0,5 соответственно). Прямая линия на графике демонстрирует веса, соответствующие нетрансформированной весовой функции.
Из графика следует, что при распределении капитала по выпуклой функции четыре комбинации с наибольшими значениями показателя имеют больший вес, чем при формировании портфеля по исходной весовой функции (эти комбинации располагаются в интервале высоких значений исходной функции, где кривая выпуклой функции проходит над прямой линией, соответствующей исходной функции). Для одной из комбинаций веса, полученные по выпуклой и исходной функциям, совпадают (эта комбинация располагается в точке пересечения исходной и выпуклой функции). Остальные комбинации при распределении капитала по выпуклой функции имеют меньший вес, чем при формировании портфеля по исходной функции (эти комбинации располагаются в интервале низких значений исходной функции, где кривая выпуклой функции проходит ниже линии исходной функции).
В том случае, когда капитал распределялся по вогнутой функции , пять комбинаций с наибольшими значениями показателя имеют меньший вес, чем при формировании портфеля по исходной функции (эти комбинации располагаются в интервале высоких значений исходной функции, где кривая вогнутой функции проходит под прямой линией, соответствующей исходной функции). Остальные 15 комбинаций имеют меньший вес, чем при формировании портфеля по исходной функции (эти комбинации располагаются в интервале низких значений исходной функции, где кривая вогнутой функции проходит выше линии исходной функции).
Читать дальше
Конец ознакомительного отрывка
Купить книгу