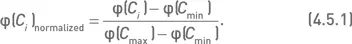Вадим Цудикман - Опционы - Разработка, оптимизация и тестирование торговых стратегий

Рассмотрим пример распределения капитала по двум показателям – математическому ожиданию прибыли и VaR. Продемонстрируем расчет мультипликативной свертки этих показателей и вычисление значений весовой функции на основе данных, приведенных в таблице 4.3.2. Поскольку эти два показателя имеют различный масштаб величин, возникает необходимость в нормализации их значений. Существует несколько способов нормализации. Мы воспользуемся формулой, позволяющей привести значения любого показателя к интервалу от нуля до единицы:

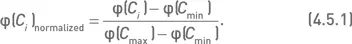
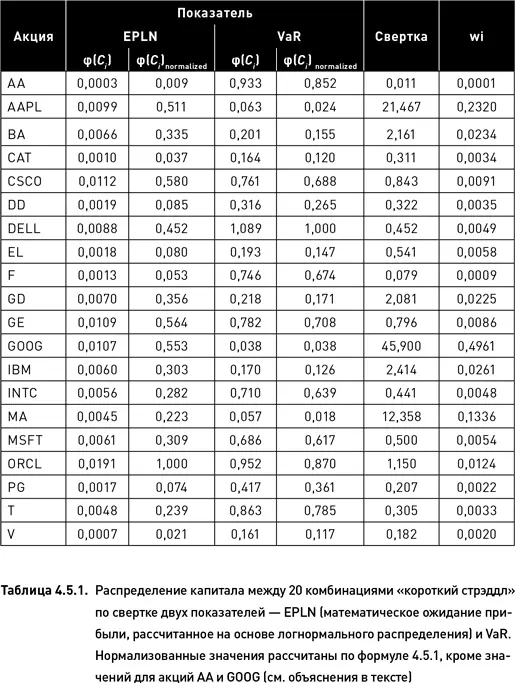
В таблице 4.5.1 приведены оригинальные значения показателя EPLN (математическое ожидание прибыли, рассчитанное на основе логнормального распределения) и VaR (взятые из таблицы 4.3.2) и их нормализованные значения, рассчитанные с помощью формулы 4.5.1. Приведем пример расчета нормализованного значения показателя EPLN для акции AAPL. Максимальное и минимальное значения EPLN составляют 0,0191 и 0,0003 соответственно. Поскольку оригинальное значение EPLN для AAPL составляет 0,0099, то, используя формулу 4.5.1, можно рассчитать нормализованное значение, как:

Поскольку показатель EPLN выражает ожидаемую прибыль, а VaR – убыток, то мультипликативная свертка рассчитывается как отношение EPLN к VaR. В этой связи возникает проблема с нулевыми значениями нормализованных показателей. Разрешить эту проблему можно путем замены нулевых значений значениями, рассчитанными по следующей формуле:

где φ( Сmin + 1 ) означает величину показателя со следующим после минимального значением. Например, по показателю EPLN нормализованная функция имеет нулевое значение для акции AA. Используя формулу 4.5.2 и учитывая, что акцией со следующим по величине показателем является V [φ( С min + 1 ) = 0,0007], можем вычислить значение нормализованного показателя для AA: (0,0003/0,0007) × 0,021 = 0,009.

После того как значения показателей нормализованы и значения свертки вычислены, остается рассчитать вес каждой комбинации в составе портфеля. Это делается с помощью формулы 4.3.5 (результаты расчетов представлены в последнем столбце таблицы 4.5.1).

В этом разделе мы проанализируем, каким образом использование многомерной системы распределения капитала влияет на параметры формируемого портфеля. Для этого необходимо сравнить прибыли портфелей, сформированных с помощью одномерной системы, с прибылями портфелей, созданных на основе многомерной системы. Такое же сравнение следует провести в отношении меры концентрированности капитала.

Мы провели сравнительный анализ на периоде 2002–2010 гг., смоделировав две торговые стратегии, аналогичные той, что была описана в разделе 4.4.1, за исключением принципа распределения капитала. В одном случае капитал распределялся по свертке двух показателей (EPLN и VaR), в другом случае – по единственному показателю EPLN. Как и в предыдущих исследованиях, на протяжении всего периода моделирования было построено 6448 портфелей для каждого из двух способов распределения капитала.

По аналогии с исследованием, описанным в разделе 4.4.3, будем рассматривать зависимость между прибылью портфеля, получаемой при распределении капитала с помощью свертки, и прибылью, получаемой при формировании портфеля на основании одного показателя. На рис. 4.5.1 по вертикальной оси отложены значения прибыли, полученной при распределении капитала по свертке двух показателей, а по горизонтальной оси – значения прибыли, соответствующие портфелям, сформированным на основании единственного показателя. Напомним, что прибыль портфелей, расположенных на линии безразличия (с коэффициентом наклона, равным 1), одинакова при распределении капитала с помощью многомерной и одномерной системы. Точки, расположенные выше линии безразличия, обозначают портфели, для которых применение многомерной систем привело к увеличению прибыли или уменьшению убытка (по сравнению с тем, что было бы, если бы капитал распределялся в соответствии с одномерной системой).