Вадим Цудикман - Опционы - Разработка, оптимизация и тестирование торговых стратегий

Задачей оптимизации является поиск такого набора весов, который максимизирует значение функции 4.6.1. Выбранная нами свертка двух показателей представляет собой нелинейную многоэксремальную конструкцию. Поэтому оптимизация осуществлялась методом Монте-Карло путем генерации случайных векторов ( w 1…, w n ) и выбора такого из них, который имеет максимальное значение функции 4.6.1. Для каждого из 6448 портфелей, сформированных на историческом периоде 2002–2010 гг., число итераций (количество сгенерированных случайных векторов ( w 1 …, w n )) составляло 10 000.

На рис. 4.6.1 показана взаимозависимость между прибылью, полученной при распределении капитала путем оптимизации свертки для всего портфеля в целом, и прибылью, получаемой при распределении капитала на основании значений свертки, вычисляемой для каждой отдельно взятой комбинации. Точки, расположенные выше линии безразличия (с коэффициентом наклона, равным 1), обозначают портфели, для которых применение портфельной системы распределения капитала привело к увеличению прибыли или уменьшению убытка (по сравнению с тем, что было бы, если бы капитал распределялся в соответствии с одномерной системой). Соответственно, точки, расположенные ниже линии безразличия, относятся к портфелям, для которых портфельная система привела к снижению прибыли или увеличению убытка.

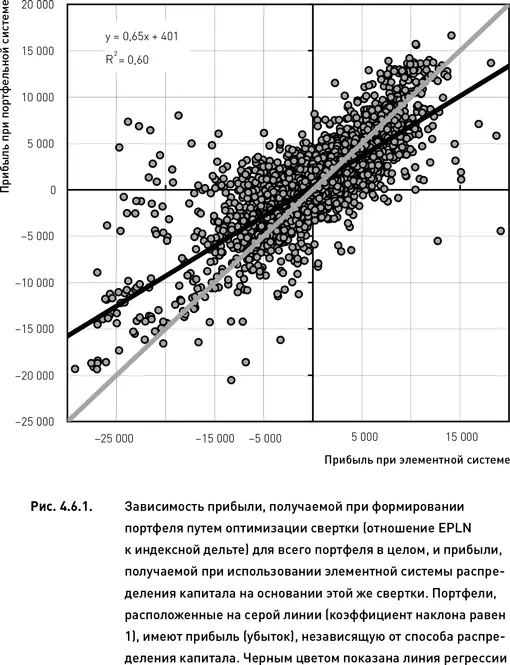
В тех случаях, когда портфель оказался прибыльным (как для портфельной, так и для элементной системы распределения капитала), большинство точек располагались ниже линии безразличия. Это означает, что распределение капитала на основании портфельной системы приводит к снижению прибыли. Однако в тех случаях, когда портфель был убыточным (для обеих систем распределения капитала), большинство точек располагались выше линии безразличия. Это указывает на то, что убытки портфелей, сформированных с помощью портфельной системы, оказались меньше убытков портфелей, основанных на элементной системе распределения капитала.

Результаты регрессионного анализа согласуются с выводами, сделанными на основании визуального анализа рис. 4.6.1. Коэффициент наклона линии регрессии равен 0,65, что значительно ниже коэффициента линии безразличия, равного 1. Хотя intercept в данном случае велик, он тем не менее достаточно мал по сравнению с общим диапазоном значений, принимаемых исследуемыми переменными. Поэтому, как и в предыдущих исследованиях, его влиянием на результаты анализа можно пренебречь. Установленная разница угловых коэффициентов статистически достоверна на высоком уровне значимости ( t = –53,5, p < 0,001). Таким образом, можно сделать вывод о том, что использование портфельной системы распределения капитала приводит к созданию более консервативного портфеля с меньшим потенциалом прибыльности и меньшим риском убытков.

Для сравнения портфельной и элементной системы распределения капитала мы воспользовались, как и в предыдущих примерах, методикой расчета индекса концентрированности портфеля, описанной в разделе 4.4.2. Для сравнения степени концентрированности капитала при формировании портфеля на основе портфельной и элементной системы воспользуемся, как и в предыдущих разделах, частотным распределением индекса концентрированности (рис. 4.6.2).

В тех случаях, когда портфели формировались на основании свертки двух показателей, рассчитанной для каждой отдельно взятой комбинации (элементная система), распределение индекса концентрированности оказалось смещенным в область низких значений индекса. Мода распределения приходится на величину индекса концентрации, равную 2 %. Это означает, что в 10 % случаев половина капитала была сконцентрирована всего в 2 % составляющих портфель комбинаций. Использование портфельной системы распределения капитала принципиально изменило форму распределения индекса концентрированности капитала (рис. 4.6.2). В этом случае распределение имеет вид, близкий по форме к нормальному, а его мода смещена в область намного более высоких значений индекса. Приблизительно в 10–12 % случаев половина капитала оказалась вложенной в 19–22 % комбинаций. Экстремальные случаи, когда половина капитала была вложена в 1–5 % комбинаций были крайне редки (менее 1 % от общего количества сформированных портфелей).