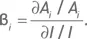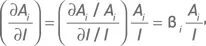Алгоритм вычисления индексной дельты можно представить в виде последовательности следующих процедур.
1. Строится регрессионная модель зависимости цены каждого базового актива (чьи опционы входят в состав портфеля) от индекса. Для этого необходимо выбрать горизонт истории, на котором строятся модели.
2. С помощью регрессионных моделей, построенных на шаге (1), рассчитываем значение цены каждого базового актива, к которому приводит изменение индекса на один пункт или на другую небольшую величину (например, на 0,1 %).
3. Определяем справедливую стоимость каждого входящего в портфель опциона при условии, что цена его базового актива равна значению, полученному на шаге (2). Для этого необходимо воспользоваться одной из моделей ценообразования, заменяя в ее формуле текущую цену базового актива соответствующим расчетным значением.
4. Вычисляем приращение цены каждого входящего в портфель опциона, произошедшее в результате изменения цены его базового актива на один пункт. Приращение цены равно разности расчетной стоимости, полученной на шаге (3), и текущей рыночной цены опциона.
5. Рассчитываем значение индексной дельты путем суммирования всех приращений, полученных при исполнении процедур на шаге (4).
Рассмотрим портфель, состоящий из опционов на различные активы. Пусть {O 1, O 2, O 3…, O N} представляет множество составляющих портфель опционов, причем базовым активом опциона O i является A i . Если при j ≠ k активы A i и A k совпадают, то речь может идти об опционной комбинации, построенной в рамках определенной торговой стратегии (например, стрэнгл, стрэддл, календарный спред и т. д.). В принципе комбинации могут состоять из неограниченного количества разных опционов, относящихся к одному базовому активу, а портфель – из неограниченного количества комбинаций.
Для каждого опциона O i , входящего в состав портфеля, мы имеем опционную дельту:
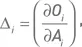
где величины δO 1и δA 1обозначают малые изменения цен опциона и его базового актива соответственно. Это выражение дает наглядное представление о дельте как о скорости изменения цены опциона по отношению к изменению цены его базового актива.
Вычисление дельты D i одного опциона не представляет сложности и реализовано во многих компьютерных программах. Переходя к портфелю, состоящему из опционов на разные базовые активы, мы не можем суммировать дельты разных опционов, поскольку они являются частными производными функций (премий) по разным независимым переменным (ценам акций). Как было сказано выше, эту задачу мы будем решать, вычисляя скорость изменения стоимости опциона по отношению к индексу, а не к отдельным базовым активам. Определим дельту по отношению к индексу как производную цены опциона по значению индекса:
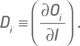
Эту индексную дельту можно также представить в следующем виде:
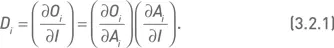
Величина 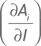 так же, как и бета показывает изменение цены базового актива при изменении индекса (разница между ними в том, что первая является размерной величиной, а вторая – безразмерной, выраженной отношением относительных изменений двух величин). Бета традиционно используется для оценки взаимосвязи между движениями индекса и отдельного актива. Для наших целей будет удобно представить бету в виде следующего отношения:
так же, как и бета показывает изменение цены базового актива при изменении индекса (разница между ними в том, что первая является размерной величиной, а вторая – безразмерной, выраженной отношением относительных изменений двух величин). Бета традиционно используется для оценки взаимосвязи между движениями индекса и отдельного актива. Для наших целей будет удобно представить бету в виде следующего отношения:
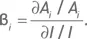
Произведя несложные преобразования
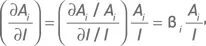
подставим полученное выражение в формулу (3.2.1). Получаем индексную дельту одного опциона:

где Δ i – дельта опциона относительно его базового актива. Количество единиц опциона O i , входящее в состав портфеля, обозначим через x i . Для вычисления индексной дельты D portfolio всего портфеля суммируем дельты отдельных опционов, входящих в портфель с учетом их количества:
Читать дальше
Конец ознакомительного отрывка
Купить книгу

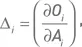
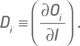
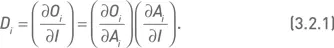
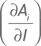 так же, как и бета показывает изменение цены базового актива при изменении индекса (разница между ними в том, что первая является размерной величиной, а вторая – безразмерной, выраженной отношением относительных изменений двух величин). Бета традиционно используется для оценки взаимосвязи между движениями индекса и отдельного актива. Для наших целей будет удобно представить бету в виде следующего отношения:
так же, как и бета показывает изменение цены базового актива при изменении индекса (разница между ними в том, что первая является размерной величиной, а вторая – безразмерной, выраженной отношением относительных изменений двух величин). Бета традиционно используется для оценки взаимосвязи между движениями индекса и отдельного актива. Для наших целей будет удобно представить бету в виде следующего отношения: