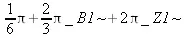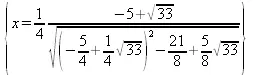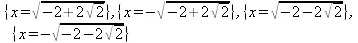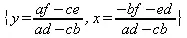1.047197551
Однако из приведенных примеров видно, что при этом найдено только одно (главное) решение. Оно ищется в интервале [-π, π]. Периодичность тригонометрических функций и связанная с этим множественность решений оказались проигнорированы. Однако можно попытаться найти все периодические решения, выполнив следующую команду:
> _EnvAllSolutions:=true;
_EnvAllSoIutions := true
Указанная в ней системная переменная отвечает за поиск всех периодических решений, когда ее значение равно true, и дает поиск только главных решений при значении false, принятом по умолчанию. Так что теперь можно получить следующее:
> solve(sin(х)=1/2,х);
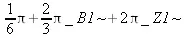
Здесь вспомогательные переменные _ВI~ и _ZI~ могут иметь только целочисленные значения (знак ~ означает, что на них наложено ограничение — в нашем случае в виде целочисленности возможных значений).
На рис. 4.31 показан более сложный случай решения нелинейного уравнения вида f 1 (х)=f 2 (x), где f 1 (х)=sin(x) и f 2 (х)=cos(x)- 1. Решение дано в графическом виде и в аналитическом для двух случаев — нахождения главных значений корней и нахождения всех корней. Обратите внимание на команду _EnvAllSolutions:=true задающую поиск всех корней.
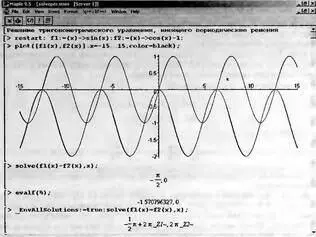
Рис. 4.31. Пример решения уравнения, имеющего периодические решения
В подобных решениях встречаются переменные _В1~ и означающие ряд натуральных чисел. Благодаря этому через них можно представить периодически повторяющиеся решения.
Примеры решения уравнений с обратными тригонометрическими функциями показаны ниже:
> eqns := 2*arcsin(x) — arccos(5*x);
eqns := 2 arcsin(x) - arccos(5x)
> solve(eqns, {x});
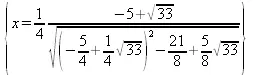
> eqns := arccos(x) — arctan(x/2);
eqns := arccos(x) - arctan(½x)
> solve(eqns, {x});
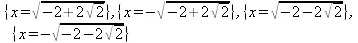
4.8.4. Решение систем линейных уравнений
Для решения систем линейных уравнений созданы мощные матричные методы, которые будут описаны отдельно в Главе 6. Однако функция solve также может успешно решать системы линейных уравнений, причем в символьном (аналитическом) виде. Такое решение в силу простоты записи функции может быть предпочтительным. Для решения система уравнений и перечень неизвестных задаются в виде множеств (см. приведенный ниже пример):
> eq1:=а*х+b*у=е; eq2:=c*x+d*y=f;
eq1 := ах + by = е
eq2 := cx + dу = f
> solve({eq1,eq2},{x,y});
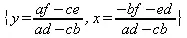
В данном случае решение системы из двух линейных уравнений представлено в символьном виде.
Рисунок 4.32 дает еще два примера решения систем из двух линейных уравнений на этот раз в численном виде. В первом примере функция solve возвращает решение в виде значений неизвестных x и у, а во втором отказывается это делать.
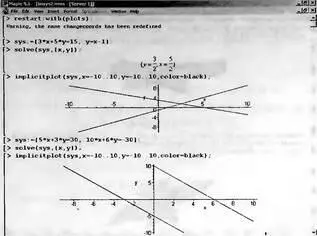
Рис. 4.32. Примеры решения системы из двух линейных уравнений с графической иллюстрацией
В чем дело? Оказывается, в том, что во втором случае система просто не имеет решения. Импликативная графика пакета расширения plots дает прекрасную возможность проиллюстрировать решение. Так, нетрудно заметить, что в первом случае геометрическая трактовка решения сводится к нахождению точки пересечения двух прямых, отображающих два уравнения. При этом имеется единственное решение, дающее значения x и у для этой точки.
Во втором случае решения и впрямь нет, ибо уравнения задают параллельно расположенные прямые, которые никогда не пересекаются. Рекомендуем читателю самостоятельно проверить и третий случай — бесконечного множества решений. Он имеет место, если оба уравнения описывают одну и ту же зависимость и их графики сливаются в одну прямую.
Решение систем из трех линейных уравнений также имеет наглядную геометрическую интерпретацию — в виде точки, в которой пересекаются три плоскости, каждая из которых описывается функцией двух переменных. Для наглядности желательно представить и линии пересечения плоскостей. Это позволяет сделать функция импликативной трехмерной графики implicitplot3d, что и показано на рис. 4.33. Для объединения графиков площадей использована функция display.
Читать дальше
Конец ознакомительного отрывка
Купить книгу