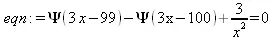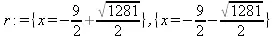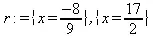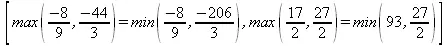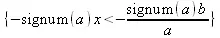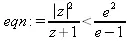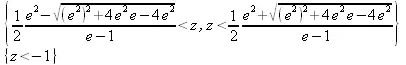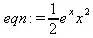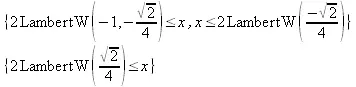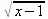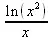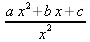4.8.7. Решение уравнений со специальными функциями
К важным достоинствам Maple относится возможность решения уравнений, содержащих специальные функции как в записи исходных выражений, так и в результатах решения. Приведем несколько примеров такого рода (файл solvesf):
> restart:eqn := Psi(3*x-99) - Psi(3*x-100) + 3/х^2=0;
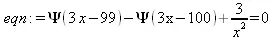
> r:=solve(eqn, {х});
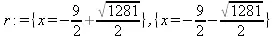
> eqn := max(x,3*x-12)=min(10*x+8, 22-x);
eqn := max(x, - 12 + 3x) = min(10x + 8, 22 - x)
> r:=solve(eqn, {x});
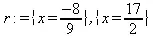
> map(subs,[r],eqn);
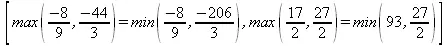
> eqn := LambertW(3*x)=ln(x);
eqn := LambertW(3x) = ln(x)
> r:=solve(eqn, {x});
r:= {x = e³}
> map(subs, [r], eqn);
[LambertW(3e³) = ln(e³)]
> evalf(map(subs,[r], eqn));
[3.000000000 = 3.000000000]
Полезно обратить внимание на не вполне обычную проверку правильности решений. Иногда при этом выводятся значения левой и правой частей уравнения, требующие осмысления полученных результатов.
4.8.8. Решение неравенств
Неравенства в математике встречаются почти столь же часто, как и равенства. Они вводятся знаками отношений, например > (больше), < (меньше) и т.д. Решение неравенств существенно расширяет возможности функции solve. При этом неравенства задаются так же, как и равенства. Приведенные на рис. 4.35 примеры поясняют технику решения неравенств.
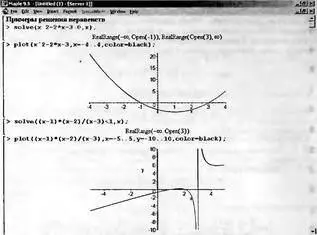
Рис. 4.35. Примеры, иллюстрирующие решение неравенств
Из приведенных примеров очевидна форма решений — представлены критические значения аргумента, вплоть до не включаемых значений области действия неравенства (они указываются словом Open). Всегда разумным является построение графика выражения, которое задает неравенство — это позволяет наглядно убедиться в правильности решения.
Приведем еще несколько примеров решения неравенств в аналитической форме (файл solveu):
> solve(5*х>10,х);
RealRange(Open(2), ∞)
> solve(5*х>=10,х);
RealRange(2, ∞)
> solve(ln(х)>2,х);
Rea1Range(Open(e²), ∞)
> solve(ехр(х)>10, х);
RealRange(Open(ln(10)), ∞
> solve(a*x>b,{х});
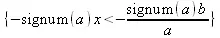
> eqn := abs(z)^2/(z+1) < ехр(2)/(ехр(1)-1);
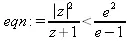
> solve(eqn, {z});
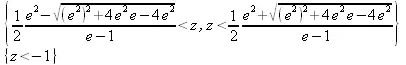
> eqn := ехр(х)*х^2 >= 1/2;
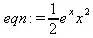
> solve(eqn, {x});
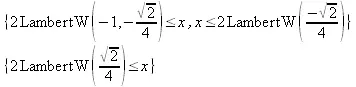
> eqns := abs((z+abs(z+2))^2-1)^2 = 9;
eqns := |(z +|z + 2|)² - 1|² = 9
> solve(eqns, {z});
{z = 0 }, { z ≤ -2}
> eqns := { х^2<1, у^2<=1, х+у<1/2 };
eqns:={х² < 1, y² ≤ 1, х + y < ½}
> solve(eqns, {x, у});
{y ≤ 1, -1 ≤ y, x+y < ½, -1 < x, x < 1}
В последнем примере показано решение системы неравенств. При этом выдаются области определения нескольких переменных.
4.8.9. Решение функциональных уравнений
Решение функционального уравнения, содержащего в составе равенства некоторую функцию f(х), заключается в нахождении этой функции. Для этого можно использовать функцию solve, что демонстрируют приведенные ниже примеры (файл solvefe):
> A:=solve(f(х)^2-х+1,f);
А := proc(x) RootOf(_Z^ 2 -х + 1, label =_L7) end proc
> convert(A(x),radical);
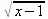
> allvalues(%);
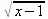
> B:=solve(f(x)*x=ln(x^2),f);
В := proc(x) ln(x^2)/x end proc
> convert(B(x),radical);
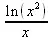
> C:=solve(f(x)*х^2=а*х^2+b*х+с, f);
C := proc(x) (ax×x^2 + bx×x + c)/x^2 end proc
> convert(C(x),radical);
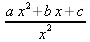
4.8.10. Решение уравнений с линейными операторами
Читать дальше
Конец ознакомительного отрывка
Купить книгу