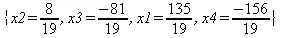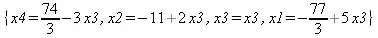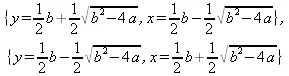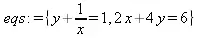Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Рис. 4.33. Пример решения системы из трех линейных уравнений с графической иллюстрацией решения

Некоторые проблемы с решением систем из трех линейных уравнений иллюстрируют примеры, приведенные на рис. 4.34. В первом примере решения вообще нет. График показывает, в чем дело — линии пересечения плоскостей идут параллельно и нигде не пересекаются. Во втором примере все три плоскости пересекаются по одной линии.

Рис. 4.34. Графическая иллюстрация особых случаев решения системы из трех линейных

Следующий пример показывает решение системы из четырех линейных уравнений:

> sys := { 4*x1 + 7*х2 - х3 + 3*х4 = 11,

-2*х1 + 2*х2 - 6*х3 4+ х4 = 4, x1 - 3*х2 + 4*x3 - х4 = -3, 3*х1 - 5*х2 - 7*х3 + 5*х4 = 8 }:

> solve(sys, {x1, х2, х3, х4});

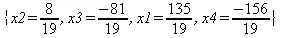
Эта система имеет решение, но его простая графическая иллюстрация уже невозможна.

Случай решения неполной системы уравнений (уравнений — 3, а неизвестных — 4) иллюстрирует следующий пример:

> sys := { x1 + 2*х2 + 3*х3 + 4*х4 = 51,

x1 - 3*х2 + 4*х3 + х4 = 32, х1 + 2*х2 - 6*х3 + х4 = -23 }:

> solve(sys, {x1, х2, х3, х4 });

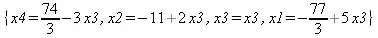
Как видно из приведенных примеров, функция solve неплохо справляется с решением систем линейных уравнений.

Функция solve может использоваться для решения систем нелинейных и трансцендентных уравнений. Для этого система уравнений и перечень неизвестных задаются в виде множеств. Ниже приведены примеры решения уравнений (файл solvenl):

> restart;

> solve{{х*у=а,x+y=b},{х,у});

> allvalues(%);

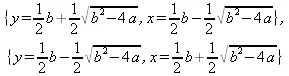
> s:=solve({x*y=2,x+y=3},{x,y});

> assign(s); x; y;

> unassign('x'); y:= 'y';

> [x, y];

В этих примерах хорошо видна техника работы с функциями solve и assign. В конце примеров показано восстановление неопределенного статуса переменных х и у с помощью функции unassign и снятие определения переменных с помощью заключения их в прямые апострофы.

Приведем еще один пример решения системы нелинейных уравнений с проверкой правильности решения с помощью функции eval:

> eqs: = {2*х+4*у=6,у+1/х=1};

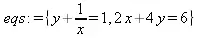
> r:=solve(eqs, {х, у});

> eval(eqs,r[1]);

> eval(eqs,r[2]);

Для проверки всех решений можно использовать также функции map и subs:

> map(subs,[r],eqs);

Maple имеет и еще ряд возможностей для проверки решений, но представленных обычно вполне достаточно для такой проверки. Ее следует принять за правило при выполнении решений уравнений.

В решениях уравнений нередко появляется функция RootOf, означающая, что корни нельзя выразить в радикалах. Эта функция применяется и самостоятельно в виде RootOf(expr) или RootOf(expr, х), где expr — алгебраическое выражение или равенство, х — имя переменной, относительно которой ищется решение. Если переменная х не указана, ищется универсальное решение по переменной _Z. Когда expr задано не в виде равенства, решается уравнение expr=0. Для получения решений вида RootOf в явном виде может использоваться функция allvalues.

Примеры применения функции RootOf (файл RootOf):

> RootOf(х^2+1=0,х);

> allvalues(%);

> RootOf(а*b^2+а/b,b);

> allvalues(%);

> RootOf(x^3-1,x) mod 7;

> allvalues(%);

> evalf(%);

> RootOf(х^2-2*х+1,х) mod 5;

Итак, функция RootOf является эффективным способом представления решения в компактном виде. Как уже отмечалось, наряду с самостоятельным применением она часто встречается в составе результатов решения нелинейных уравнений.