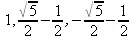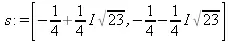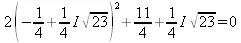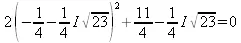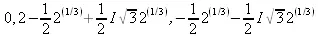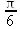Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Характер решений можно изменить с помощью глобальных системных переменных:

_EnvExplicit — при значении true выдает решение без применения конструкции RootOf;

_EnvAllSolutions — при значении true задает выдачу всех решений;

_SolutionsMayBeLost — при значении true дает решение, которое при обычном применении функции solve возвращает значения NULL;

_MaxSols — задает максимальное число решений;

_EnvTryHard — при значении true может дать компактное решение, но это может потребовать увеличения времени вычислений.

В решениях могут встречаться следующие обозначения:

_NN — указывает на неотрицательные решения;

_В — указывает на решения в бинарной форме;

_Z — указывает на то, что решение содержит целые числа;

%N — при текстовом формате вывода задает общие члены решения и обеспечивает более компактную форму его представления.

В форме solve[subtopic] возможны параметры subtopic функции solve следующих типов:

floats functions identity ineq linear

radical scalar series system

При решении систем уравнений они и список переменных задаются как множества, то есть в фигурных скобках. При этом и результат решения получается в виде множества. Чтобы преобразовать его к обычному решению, нужно использовать функцию assign, которая обеспечивает присваивание переменным значений, взятых из множества.

Функция solve старается дать решение в аналитическом виде. Это не означает, что ее нельзя использовать для получения корней уравнений в численном виде. Просто для этого придется использовать функции evalf или convert. Если результат решения представлен через функцию RootOf, то зачастую можно получить все корни с помощью функции allvalues.

Решение одиночных нелинейных уравнений вида f(х)=0 легко обеспечивается функций solve(f(x),x). Это демонстрируют следующие примеры (файл solve):

> solve(х^3-2*х+1,х);

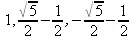
> solve(х^(3/2)=3,х);

> evalf(%);

> solve(sqrt(ln(х))=2,х);

> evalf(%);

Если уравнение записывается без правой части, то это означает, что она равна нулю. Часто бывает удобно представлять уравнение и его решение в виде отдельных объектов, отождествленных с определенной переменной (файл solve):

> eq:=(2*х^2+х+3=0);

> s: = [solve(eq,x)];

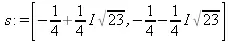
В частности, это позволяет легко проверить решение (даже если оно не одно, как в приведенном примере) подстановкой (subs):

> subs(x=s[1],eq);

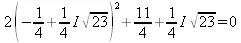
> subs(x=s[2],eq);

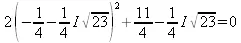
> evalf(%);

Сводящиеся к одному уравнению равенства вида f 1 (х)=f 2 (x) также решаются функцией solve(f1(x)=f2(x),x):

> solve(х^4=-х-1,х);

> evalf(%);

> solve({exp(x)=sin(x)},x);

> evalf(%);

> solve(x^4=2*x,x);

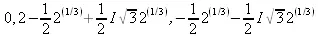
> evalf(%);

Обратите внимание в этих примерах на эффективность применения функции evalf, позволяющей получить решения, выраженные через функцию RootOf, в явном виде.

Некоторые даже с виду простые уравнения могут дать неожиданные для многих пользователей результаты. Пример такого рода приведен ниже (файл solve):

> restart;eq:=ехр(-х)=х;sol:=solve(exp(-х)=х,х);

> evalf(sol);

В данном случае решение получено через значение специальной функции Ламберта. Впрочем, с помощью функции evalf его можно представить в численном виде.

Функция solve может использоваться для решения тригонометрических уравнений:

> solve (sin (х) =.2, х);

> solve(sin(х)-1/2,х);

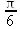
> solve(cos(х)=.5, х);