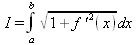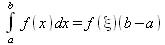Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Данный инструмент позволяет наблюдать в анимации повышение точности вычислений по мере увеличения числа прямоугольников — см. рис. 4.21. Для пуска анимации достаточно нажать мышью кнопку Animate. На рис. 4.21 показан промежуточный кадр анимации. В конце анимации закраска области интегрирования становится сплошной, после чего анимация циклически повторяется.

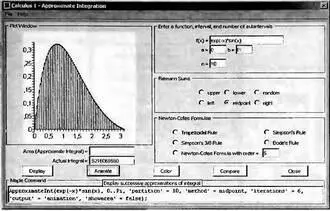
Рис. 4.21. Промежуточный кадр анимации, демонстрирующей приближение интеграла суммами Римана

Приближение суммами Римана относится к довольно медленным методам интегрирования. Значительно повысить скорость интегрирования при заданной погрешности позволяют методы интегрирования повышенного порядка на основе формул Ньютона-Котесса. На рис. 4.22 показан пример приближения определенного интеграла на основе формулы Симпсона (параболического приближения подынтегральной функции). Из рисунка хорошо видно, что в этом случае (в отличие от рис. 4.20 при интегрировании методом прямоугольников) исходная подынтегральная функция и ее приближение отрезками парабол практически совпадают и на глаз их отличия выявить трудно.

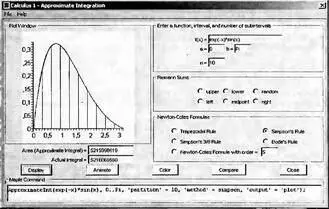
Рис. 4.22. Пример приближения интеграла методом Симпсона

Кнопка Compare позволяет вывести таблицу с данными сравнения результатов интегрирования различными методами. Окно с этой таблицей представлено на рис. 4.23. Хорошо видно, что по мере повышения порядка метода интегрирования погрешность интегрирования уменьшается.

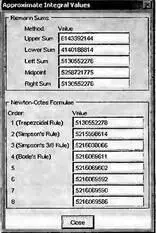
Рис. 4.23. Окно с результатами сравнения интегрирования различными методами

Если f(x) непрерывная на отрезке от а до b функция, то длина дуги этой функции (длина спрямленного отрезка) определяется известным выражением:

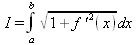
Для демонстрации вычисления длины дуги заданной аналитической функции имеется Maplet-инструмент ArcLench. Для вызова его окна (рис. 4.24) нужно исполнить команду (в стандартном варианте интерфейса): Tools→Tutors→Calculus-Single Variables→ArcLench….

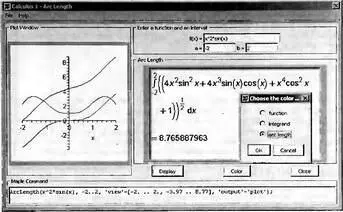
Рис. 4.24 Окно Maplet-инструмента для вычисления длины дуги

Данный инструмент по заданной функции f(x) и значениям а и b вычисляет длину дуги, выводит ее значение и вид интеграла, а также строит график функции, ее производной и зависимости длины дуги, начинающейся в точке а от текущего значения х, меняющегося от а до b. Соответствующие графики, отличающиеся цветом кривых, показываются в левой части окна инструмента.

Кнопка Color открывает окно выбора цвета из списка, который представлен окном Choose the color…, показанным внутри окна инструмента (см. рис. 4.24).

Выбрав цвет нужной кривой нажатие кнопки OK можно вызвать панель выбора цветов Select a color, показанную на рис. 4.25. По завершении выбора цвета нужная кривая будет отображена в новом цвете.

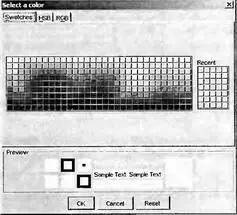
Рис. 4.25 Панель выбора цвета

Первая теорема о среднем гласит, что если f(x) интегрируемая функция, непрерывная на отрезке [a, b], то существует по крайней мере одно значение х=ξ в интервале [a, b], при котором

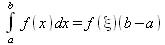
Иными площадь, определяемая интегралом может быть вычислена как площадь прямоугольника с основанием — отрезком ab и высотой f(ξ).

Для иллюстрации этого положения служит Maplet-инструмент Mean Value Theorem. Его окно (рис. 4.26) открывается исполнением команды Tools→Tutors Calculus-Single Variables→Mean Value Theorem… Работа с окном вполне очевидна. На графике строится кривая функции, отрезок, проходящий через ее концевые точки, точка со значением х=с=ξ и касательная к ней. Главный результат — значение с=ξ .

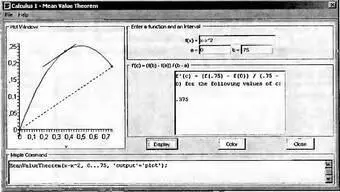
Рис. 4. 26. Окно Maplet-инструмента для иллюстрации первой теоремы о среднем