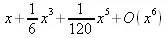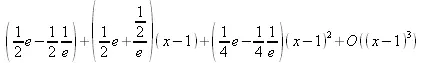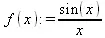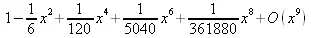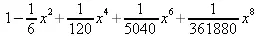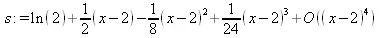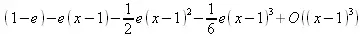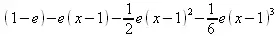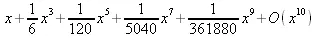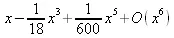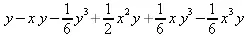Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Для разложения функции или выражения expr в обычный степенной ряд в системе Maple служат функции:

series(expr, eqn)

и

series(expr, eqn, n)

Здесь expr — разлагаемое выражение, eqn — условие (например, в виде х=а) или имя переменной (например, х) и n — необязательное и неотрицательное целое число, задающее число членов ряда (при его отсутствии оно по умолчанию берется равным 6, но может переустанавливаться системной переменной Order). Если в качестве eqn задано имя переменной, то это соответствует разложению по этой переменной в области точки с ее нулевым значением. Задав eqn в виде x=x0 можно получить разложение по переменной х в окрестности точки x=х 0.

Разложение получается в форме степенного многочлена, коэффициенты которого задаются рациональными числами. Остаточная погрешность задается членом вида O(х)^n. При точном разложении этот член отсутствует. В общем случае для его удаления можно использовать функцию convert. Ниже представлены примеры разложения различных выражений в ряд (файл series):

> series(sinh(х), х=0);

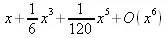
> series(sinh(х),х=1,3);

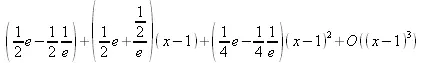
> series(sinh(х),х=1.0,3);

> series(2*х^2-х+1,х=1,10);

> f(х):=sin(х)/х;

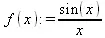
> series(f(х),х=0,10);

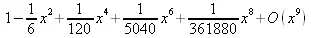
> convert(%,polynom);

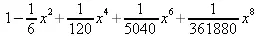
> s:=series(ln(х),х=2, 4);

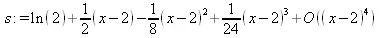
> evalf(convert(s,polynom));

Здесь видно, что член, обозначающий погрешность, отсутствует в тех разложениях, которые точны — например, в разложениях степенных многочленов.

Для разложения в ряд Тейлора используется функция taylor(expr, eq/nm, n). Здесь expr — разлагаемое в ряд выражение, eq/nm — равенство (в виде х=а) или имя переменной (например, х), n — необязательный параметр, указывающий на порядок разложения и представленный целым положительным числом (при отсутствии указания порядка он по умолчанию принимается равным 6). При задании eq/nm в виде x=a разложение производится относительно точки x=a. При указании eq/nm в виде просто имени переменной разложение ищется в окрестности нулевой точки, то есть фактически вычисляется ряд Маклорена.

Ниже представлены примеры применения функции taylor (файл taylor):

> taylor(1-ехр(х), х=1, 4);

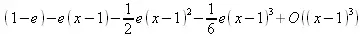
> convert(%,polynom);

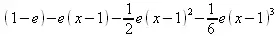
> taylor(sinh(x), x, 10);

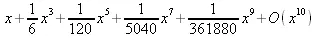
> taylor(int(sin(x)/x,x),x);

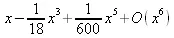
> taylor(erf(х),х);

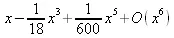
Не все выражения (функции) имеют разложение в ряд Тейлора. Ниже дан пример такого рода:

> taylor(1/х+х^2,х,5);

Error, does not have a taylor expansion, try series()

> series(1/х+х^2,x,10);

> taylor(1/х+х^2,x=1,5);

Здесь Maple 9.5 отказался от вычисления ряда Тейлора в окрестности точки х=0 (по умолчанию) и предложил воспользоваться функцией series. Однако эта функция просто повторяет исходное разложение. В то же время в окрестности точки х=1 ряд Тейлора вычисляется.

Для разложения в ряд Тейлора функций нескольких переменных используется библиотечная функция mtaylor:

mtaylor(f, v)

mtaylor(f, v, n)

mtaylor(f, v, n, w)

Здесь f — алгебраическое выражение, v — список имен или равенств, n — необязательное число, задающее порядок разложения, w — необязательный список целых чисел, задающих «вес» каждой из переменных списка v. Эта функция должна вызываться из библиотеки Maple 9 с помощью команды readlib:

> readlib(mtaylor); mtaylor(sin(х*у),[х,у],10,[2,1]);

> mtaylor(exp(-x)*sin(y),[x,y],5);

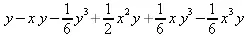
Для получения только коэффициента при k- м члене ряда Тейлора можно использовать функцию coeftayl(expr,var,k). Если expr — функция нескольких переменных, то k должен задаваться списком порядков коэффициентов.