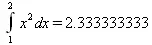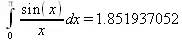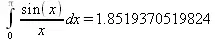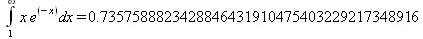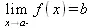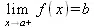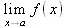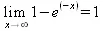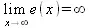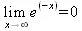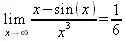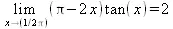Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

> Int(х^2,х=1..2)=evalf(Int(х^2,х=1..2));

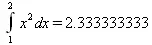
> Int(sin(x)/x,х=0..Pi)=evalf(int(sin(х)/х,х=0..Pi));

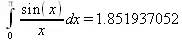
> Digits:=15;Int(sin(x)/x,x=0..Pi)=evalf(int(sin(x)/x, x=0..Pi, method = _NCrule));

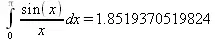
> expr := x*exp(-x):

Int(expr, x=1..infinity) = evalf[40](Int(expr, x=1..infinity, method=_Gquad));

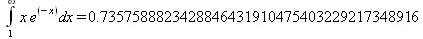
В двух последних примерах показано вычисление интегралов с повышенной точностью в 15 и 40 верных знаков. Аналогичным образом могут вычисляться и кратные интегралы.

На время и возможность вычисления определенных интегралов большое значение оказывает выбранный метод вычислений. Нередко его стоит указывать явно. Ниже приведены примеры этого с оценкой времени интегрирования (файл intmet):

> restart: t:=time(): int((1-ехр(-z^2))/(BesselJ(1, z)^2+ BesselY(1,z)^2)/z^3,z=0.0..infinity); time()-t;

> t:=time(): evalf(Int((1-ехр(-z^2))/(BesselJ(1, z)^2+ BesselY(1,z)^2)/z^3,z=0..infinity, Gquad)); time()-t;

> t: =time(): evalf(Int((1-exp(-z^2))/(BesselJ(1, z)^2+ BesselY(1,z)^)/z^3,z=0.. infinity,_CCquad)); time()-t;

> t:=time(): evalf(Int((1-ехр(-z^2))/(BesselJ(1,z)^2+ BesselY(1,z)^2)/z^3,z=0..infinity,_Sinc)); time()-t;

> t:=time(): evalf(Int((1-ехр(-z^2))/(BesselJ(1, z)^2+ BesselY(1,z)^2)z^3,z=0..infinity,_Dexp)); time()-t;

В данном случае лучшим оказался метод _Dexp (адаптивный двойной экспоненциальный метода). Разумеется, для других интегралов более целесообразным может оказаться применение другого метода. Приведенные значения времен интегрирования могут заметно отличаться при реализации вычислений на разных ПК. Данные выше приведены для ПК с процессором Pentium 4 НТ с рабочей частотой 2,6 ГГц.

Пределом функции f(х) называют то ее значение b, к которому функция неограниченно приближается в точке х=а (предел в точке) или слева или справа от нее. Пределы обозначается как:

Предел в точке a	Предел слева от точки a	Предел справа от точки а

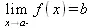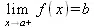При этом подразумевается, что функция f(x) определена на некотором промежутке, включающем точку х=а и во всех точках, близких к ней слева и справа. В последнем случае предел вычисляется для х=а-h или x=a+h при h стремящемся к нулю. Пределом может быть число, математическое выражение и положительная или отрицательная бесконечность. Последнее соответствует расширенному представлению о пределах.

Для вычисления пределов функции f в точке х=а используются следующие функции:

limit(f,x=a);

limit(f,x=a,dir);

Limit(f,x=a);

Limit(f,x=a,dir);

Здесь f — алгебраическое выражение, z — имя переменной, dir — параметр, указывающий на направление поиска предела (left — слева, right — справа, real — в области вещественных значений, complex — в области комплексных значений). Значением а может быть бесконечность (как положительная, так и отрицательная).

Примеры применения этих функций для вычисления пределов в точке приведены ниже (файл limit):

> restart: Limit(f(х),х=а);

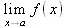
> Limit(1-ехр(-х), x=infinity)=limit(1-exp(-x), x=infinity);

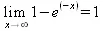
> Limit(exp(x),x=infinity) = limit(exp(x),x=infinity);

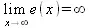
> Limit(exp(-x),x=infinity)=limit(exp(-x),x=infinity);

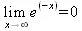
> Limit((x-sin(x))/x^3, x=0)=limit((x-sin(x))/х^3,х=0);

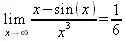
> Limit((Pi-2*x)*tan(x),x=Pi/2)=limit(tan(x)*(Pi-2*x), x=Pi/2);

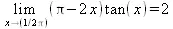
Обратите внимание на то, что в первом примере фактически дано обозначение предела в самом общем виде. Приведем еще пример вычисления предела функции в виде дроби, имеющей неопределенность 0/0: