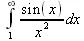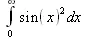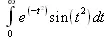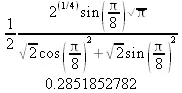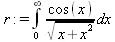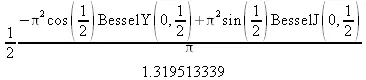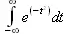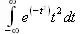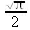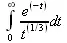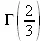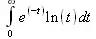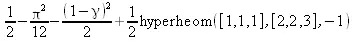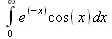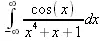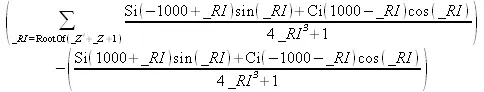Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Последние версии Maple существенно продвинулись в направлении решения многих несобственных интегралов. Это видно из благополучного решения ряда таких несобственных интегралов первого рода, о которых спотыкались старые версии Maple и которые требуют специальных решений (файл intspec) :

> Int(sin(х)/х^2,х=1..infinity);

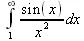
> value(%);evalf(%);

> Int(sin(x)^2,х=0..infinity);

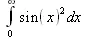
> value(%);

> Int(exp(-t^2)*sin(t^2),t=0..infinity);

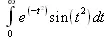
> value(%);evalf(%);

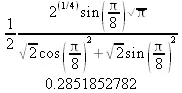
> r:=Int(cos(x)/sqrt(х+х^2),x=0..infinity);

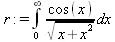
> value(r);evalf(r11);

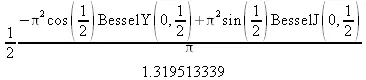
> Int(ехр(-t^2), t=-infinity..infinity);

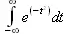
> value(%);

> Int(exp(-t^2)*t*2, t=-infinity..infinity);

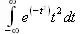
> value(%);

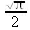
> Int(exp(-t)/t^(1/3), t=0..infinity);

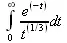
> value(%);

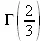
> Int(exp(-t)*ln(t),t=0..infinity);

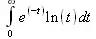
> value(%);

> Int(exp(-t)*ln(t)/t=1..infinity);

> value(%);

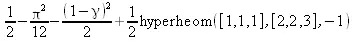
> evalf(%);

> Int(exp(-x)*cos(x),x=0..infinity);

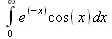
> value(%);

Для подавляющего большинства интегралов результат вычислений с применением функций Int и int оказывается абсолютно идентичным. Однако есть и исключения из этого правила. Например, следующий интеграл благополучно очень быстро вычисляется функцией Int с последующей evalf:

> Int(cos(х)/(x^4+x+1),x=-infinity..infinity);

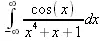
> evalf(%);

Однако в Maple 9 функция int вместо числа возвращает «страшное» выражение:

> int(cos(х)/(х^4+х+1),x=-infinity..infinity);

Увы, но функция evalf(%), примененная после него, к более простому выражению не приводит — она просто повторяет выражение в выходной строке. Maple 9.5 при вычислении этого интеграла просто «завис» и спустя минуту так и не выдал результат.

Построив график подынтегрального выражения (проделайте это сами) можно убедиться в том, он представляет собой сильно затухающую волну с узким высоким пиком в точке x=1. Попытаемся выполнить интегрирование в достаточно больших, но конечных пределах, где волна почти полностью затухает:

> int(cos(х)/(х^4+х+1),х=-1000..1000);

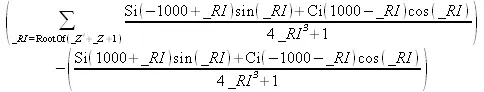
> evalf(%);

На сей раз результат получен (Maple 9.5 затратил на это около секунды). Он очень близок к полученному функцией Int, но все же имеет подозрительную мнимую часть с вроде бы нулевым значением. Он показывает, что не все здесь благополучно и что «пенки» в вычислении некоторых интегралов в Maple 9.5 все же возможны.

К несобственным интегралам второго рода относятся интегралы, имеющие в пределах интегрирования особенности подынтегральной функции. При этом сами пределы могут быть и конечными. Некоторые интегралы не имеют в среде Maple 9.5 общего решения, но исправно вычисляются для частных случаев (см. ниже для n неопределенного и конкретного n=6):