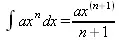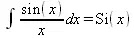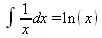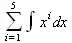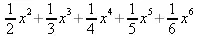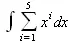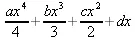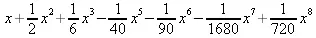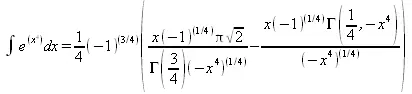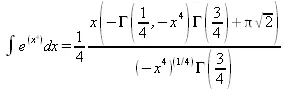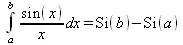Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Int(f,x); Int(f,x=a..b);

Int(f,x=a..b,continuous);

Здесь f — подынтегральная функция, x — переменная, по которой выполняются вычисления, а и b — нижний и верхний пределы интегрирования, continuous — необязательное дополнительное условие.

Maple старается найти аналитическое значение интеграла с заданной подынтегральной функцией. Если это не удается (например, для «не берущихся» интегралов), то возвращается исходная запись интеграла. Ниже приведены примеры визуализации и вычисления неопределенных интегралов (файл intex):

> Int(a*x^n,x)=int(а*х^n,х);

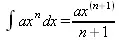
> Int(sin(х)/х,х)=int(sin(х)/х,х);

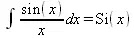
> Int(ln(х)^3,х);

> value(%);

> Int(х^5*ехр(-х),х);

> value(%);

> Int(1/х,x)=int(1/х,х);

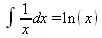
Обратите внимание, что в аналитическом представлении неопределенных интегралов отсутствует произвольная постоянная С. Не следует забывать о ее существовании.

Возможно вычисление сумм интегралов и интегралов сумм, а также интегралов от полиномов.

> Sum(Int(x^i,х),i=1..5);

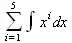
> value(%);

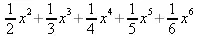
> Int(sum(х^i, i=1..5),x);

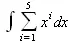
> value(%);

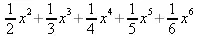
> Р(х):=а*х^3+b*х^2+с*х+d;

> int(Р(х),х);

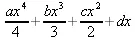
Maple 9.5 успешно берет большинство справочных интегралов. Но не всегда форма представления интеграла совпадает с приведенной в том или ином справочнике.

В некоторых случаях Maple не может вычислить интеграл. Тогда он просто повторяет его. С помощью функций taylor и convert можно попытаться получить аналитическое решение в виде полинома умеренной степени, что демонстрирует следующий характерный пример:

> int(exp(sin(х)),х);

> convert(taylor(%,х=0,8),polynom);

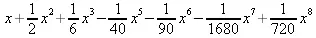
Естественно, что в этом случае решение является приближенным, но оно все же есть и с ним можно работать, например, можно построить график функции, представляющей данный интеграл.

Система Maple непрерывно совершенствуется. Например, в Maple V R4 интеграл с подынтегральной функцией ехр(х^4) не брался, а системы Maple, начиная с версии Maple 7, с легкостью берут его:

> Int(exp(x^4),х)=int(exp(х^4),х);

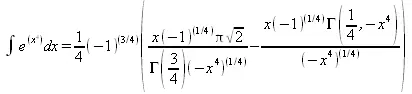
Хотя полученный результат, выраженный через гамма-функцию, нельзя назвать очень простым, но он существует и с ним также можно работать. Например, можно попытаться несколько упростить его, используя функцию simplify:

> simplify(%);

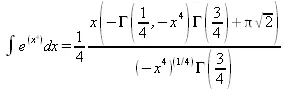
Разумеется, существует также множество иных возможностей и приемов для выполнения операции интегрирования. В дальнейшем мы неоднократно будем рассматривать и другие, более специфические функции для осуществления интегрирования и вычисления интегральных преобразований. В частности, ряд средств вычисления интегралов реализован в пакете student.

Для вычисления определенных интегралов используются те же функции int и Int, в которых надо указать пределы интегрирования, например. х=а..b, если интегрируется функция переменной х . Это поясняется приведенными ниже примерами:

> Int(sin(x)/x,х=а..b)=int(sin(х)/х,х=а..b);

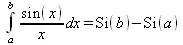
> Int(sin(х)/х,х=0..1.)=int(sin(х)/х, х=0..1.);