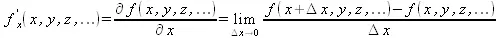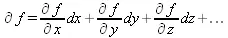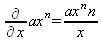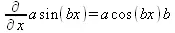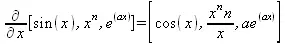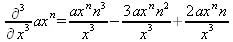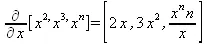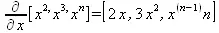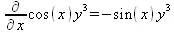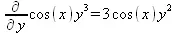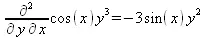Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

строят график синусоиды и касательной к ней в точке х=1.7.

Помимо производной, часто встречается понятие дифференциала

то есть произведения производной функции на приращение ее аргумента Δx→0.

Производная от производной f(x), то есть функция f''(x) называется производной второго порядка. Могут быть производные третьего, четвертого и так далее, словом производные высшего порядка. Все математические системы способны вычислять такие производные, как и первую производную f'(x) от функции f(x).

Довольно часто встречаются функции ряда переменных, например f(x, у, z, …) . В этом случае может идти речь о частных производных по переменным х, у , z , …. Например, частной производной по переменной х будет выражение:

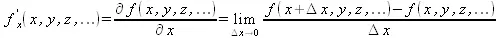
Подобные выражения нетрудно составить и для частных производных по другим переменным. Можно считать, что при вычислении частной производной по какой то переменной остальные переменные рассматриваются просто как константы. Можно также говорить о частных дифференциалах. Полный дифференциал функции многих переменных можно определить как:

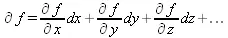
Системы символьной математики позволяют вычислять производные как символьной, так и в численной форме.

Выражение (4.1) показывает, что производная f'(x) может быть найдена путем вычисления предела, записанного в (4.1). Этот популярный у математиков метод получил название Δ -метода. В СКМ он используется редко, поскольку они имеют прямые операторы или функции для вычисления производных.

Для вычисления производных Maple имеет следующие основные функции:

diff(a, x1, х2, ..., xn)

diff(a, [x1, х2, ..., хn])

Diff(a, x1, х2, ..., xn)

Diff(a, [x1, х2, ..., xn])

Здесь а — дифференцируемое алгебраическое выражение, в частности, функция f(x1, х2, хn) ряда переменных, по которым производится дифференцирование. Функция Diff является инертной формой вычисляемой функции diff и может использоваться для естественного воспроизведения производных в документах.

Первая из этих функций (в вычисляемой и в инертной форме) вычисляет частные производные для выражения а по переменным х1, х2, …, хn. В простейшем случае diff(f(x),x) вычисляет первую производную функции f(x) по переменной х. При n, большем 1, вычисления производных выполняются рекурсивно, например, diff(f(x), х, у) эквивалентно diff(diff(f(x), х), у). Оператор $ можно использовать для вычисления производных высокого порядка. Для этого после имени соответствующей переменной ставится этот оператор и указывается порядок производной. Например, выражение diff(f(x),x$4) вычисляет производную 4-го порядка и эквивалентно записи diff(f(x),x,x,x,x). A diff(g(x,y),x$2,y$3) эквивалентно diff(g(x,y),x,x,y,y,y).

Примеры визуализации и вычисления производных (файл diff):

> restart;

> Diff(a*x^n,x)=diff(а*х^n,х);

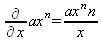
> Diff(a*sin(b*x),x)=diff(a*sin(b*x),x);

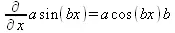
> Diff([sin(x),х^n,ехр(a*x)], x)=diff([sin(x),x^n, exp(a*x)], x);

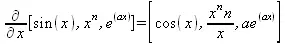
> Diff(а*х^n,x$3)=diff(а*х^n,x$3);

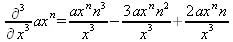
> Diff([х^2,х^3,х^n],x)=diff([х^2,х^3,х^n],x);

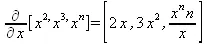
> simplify(%);

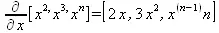
Как видно из приведенных примеров, функции вычисления производных могут использоваться с параметрами, заданными списками. Приведенные ниже примеры показывают эти возможности и иллюстрируют дифференцирование функции пользователя для двух переменных:

> restart;

> f(х,у):=cos(х)*у^3;

> Diff(f(х, y), x) = diff(f(x, y), x);

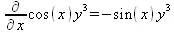
> Diff(f(x, у), y) = diff(f(x, у), y);

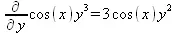
> Diff(f(x,y),x,y)=diff(f(x,у),x,y);

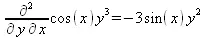
> Diff(f(x,y),x$4)=diff(f(x,y), x$4);