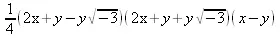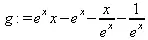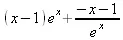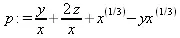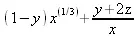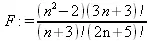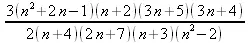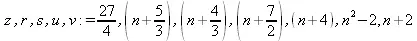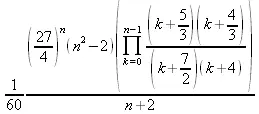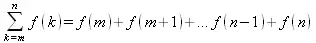α
> factor(х^2-2,alpha);
(х + α)(х - α)
> factor(х^3-у^3);
(х - у)(х² + ху + y²)
> factor(х^3-у^3, (-2)^(1/2));
(x - y)(x² + ху + y²)
> factor(х^3-у^3, (-3)^(1/2));
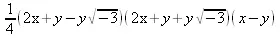
> factor(х^3-3,complex);
(х+.7211247852 + 1.249024766I)(х+.7211247852 - 1.249024766I) (х - 1.442249570)
3.7.5. Комплектование по степеням — collect
Еще одна функция общего назначения — collect — служит для комплектования выражения expr по степеням указанного фрагмента х (в том числе множества либо списка). Она задается в одной из следующих форм:
collect(а, х)
collect(а, х, form, func)
Во второй форме этой функции дополнительно задаются параметры form (форма) и func (функция или процедура). Параметр form может иметь два значения: recursive (рекурсивная форма) и distributed (дистрибутивная форма). Параметр func позволяет задать имя функции, по которой будет идти комплектование expr. Примеры применения функции collect представлены ниже (файл collect):
> collect(х+х^3-2*х,х);
-x + x³
> collect(х+2*у^3+х+3+х^3*у,recursive, х);
х(2х + 2у³ + 3 + х³y)
> collect(х+2*у^3+х+3+х^3*у,distributive,у);
у(2х + 2y³ + 3 + х³y)
> f:=а*ехр(х)-ехр(х)*х-х;
f: = ае х- е x- х
> collect(f,ехр(х));
(а - х)е х- х
> g:=int(х*(ехр(х)+ехр(-х)),х);
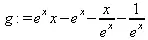
> collect(g,ехр(х));
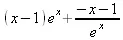
> р:=х*у+а*х*у+у*х^2-а*у*х^2+х+а*х;
р:= ху + аху + уx² - аух² + х + ах
> collect(р,[х,у],recursive);
(1 - а)ух² + ((1 + а)у + 1 + а)х
> collect(р,[х,у],distributed);
(1 +а)х + (1 + а)ху + (1 - а)ух²
> f:=а^3*х^2-х+а^3+а;
f:= а³х² - х + а³ + а
> collect(f,х);
а³х² - х + а³ + а
> collect(f,х,factor);
а³х² - х + а(а² + 1)
> p:=y/x+2*z/x+x^(1/3)-у*х^(1/3);
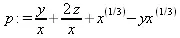
> collect(р,х);
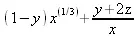
3.7.6. Работа с пакетом рациональных нормальных форм RationalNormalForms
В Maple входит пакет рациональных нормальных форм RationalNormalForms:
> with(RationalNormalForms);
[AreSimilar, IsHypergeometricTerm, MinimalRepresentation, PolynomialNormalForm, RationalCanonicalForm]
Этот пакет обеспечивает следующие возможности:
• конструирование полиномиальных нормальных форм рациональных функций;
• конструирование рациональных канонических форм для рациональных функций;
• конструирование минимальных представлений для гипергеометрических термов.
Ввиду очевидности названий функций этого пакета ограничимся примерами его применения (файл rnform):
> F := (n^2-2)*(3*n+3)!/((n+3)!*(2*n+5)!);
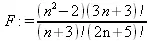
> IsHypergeometricTerm(F,n,'certificate');
true
> certificate;
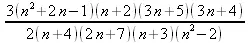
> (z,r,s,u,v) := RationalCanonicalForm[1](certificate,n);
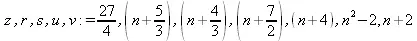
> MinimalRepresentation[1](F,n,k);
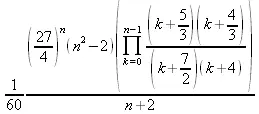
Глава 4
Практика математического анализа
Математический анализ — одна из самых благодатных областей применения систем компьютерной алгебры [36–46]. В этой главе описано решение с помощью СКА Maple наиболее важных задач математического анализа. Особое внимание в этой главе уделено визуализации записи исходных выражений и результатов вычислений, а также проверке последних.
4.1. Вычисление сумм последовательностей
4.1.1. Основные функции для вычисления сумм последовательностей
Начнем рассмотрение задач математического анализа с вычисления сумм последовательностей. Вычисление суммы членов некоторой последовательности f(k) при изменении целочисленного индекса k от значения m до значения n с шагом +1, то есть выражения
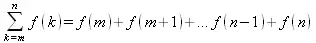
является достаточно распространенной операцией математического анализа. Для вычисляемой и инертной форм сумм последовательностей служат следующие функции:
Читать дальше
Конец ознакомительного отрывка
Купить книгу