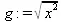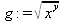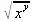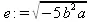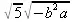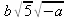Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

> X[1];

> X[1..2];

> X[-2..-1];

> S:={a,b,c};

> S[1];

> S[3];

> S[1..2];

> S[-2..-1];

Функция simplify — одна из самых мощных в системах символьной математики. Она предназначена для упрощения математических выражений. «Все гениальное просто» — любим мы повторять, хотя это далеко не всегда так. Тем не менее, стремление представить многие математические выражения в наиболее простом виде поощряется в большинстве вычислений и нередко составляет их цель.

В системе Maple функция упрощения используется в следующем виде:

• simplify(expr) — возвращает упрощенное выражение expr или повторяет его, если упрощение в рамках правил Maple невозможно;

• simplify(expr, n1, n2, …) — возвращает упрощенное выражение expr с учетом параметров с именами n1, n2, … (в том числе заданных списком или множеством);

• simplify(expr,assume=prop) — возвращает упрощенное выражение expr с учетом всех условий, представленных равенством или списком равенств.

Функция simplify — многоцелевая. Она обеспечивает упрощение математических выражений, выполняя следующие типовые действия (для простоты обозначим их как ->):

• комбинируя цифровые подвыражения (3*х*5->15*х, 10*x/5->2*x);

• приводя подобные множители в произведениях (х^3*а*х->а*х^4);

• приводя подобные члены в суммах (5*х+2+3*х->8*х+2);

• используя тождества, содержащие ноль (а+0->а, х-0->х);

• используя тождества, содержащие единицу (1*х->х);

• распределяя целочисленные показатели степени в произведениях ((3*х*у^3)^2->9*х^2*у^6);

• сокращая expr на наибольший общий полиномиальный или иной множитель;

• понижая степень полиномов там, где это возможно;

• используя преобразования, способные упростить выражения.

Несмотря на свою гибкость, функция simplify не всегда способна выполнить возможные упрощения. В этом случае ей надо подсказать, в какой области ищутся упрощения и где можно найти соответствующие упрощающие преобразования. С этой целью в функцию simplify можно включать дополнительные параметры.

В качестве параметров могут задаваться имена специальных математических функций и указания на область действия упрощений: BesselI, BesselJ, BesselK, BesselY, Ei, GAMMA, RootOf, LambertW, dilog, exp, ln, sqrt, polylog, pg, pochhammer, trig (для всех тригонометрических функций), hypergeom, radical, power и atsign (для операторов).

Полезен также параметр symbolic, задающий формальные символьные преобразования для многозначных функций, например, таких как квадратный корень (примеры из файла simplify):

> g:=sqrt(х^2);

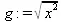
> simplify(g);

> simplify(g,assume=real);

> simplify(g,assume=positive);

> simplify(g,symbolic);

Но, чуть иначе:

> g:=sqrt(х^у);

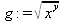
> simplify(g);

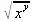
> simplify(g,assume=real);

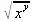
> simplify(g,assume=positive);

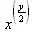
> simplify(g,symbolic);

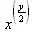
Возможно также применение функции simplify в форме simplify[] где — одно из следующих указаний: atsign, GAMMA, hypergeom, power, radical, RootOf, sqrt, trig.

Ниже даны примеры применения функции simplify:

> simplify(4^(1/2)+3);

> simplify((х^у)^z+3^(3),power);

> simplify(sin(х)^2+cos(х)^2,trig);

> e:=cos(х)^5+sin(х)^4+2*cos(х)^2-2*sin(х)^2-cos(2*х);

> simplify(e);

> simplify(GAMMA(n+4)/GAMMA(n),GAMMA);

> r:=RootOf(х^2-2=0,х):

> simplify(r^2,RootOf);

> simplify(1/r,RootOf);

> simplify(ln(x*y),power,symbolic);

> е:=(-5*b^2*а)^(1/2);

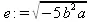
> simplify(e,radical);

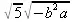
> simplify(e,radical,symbolic);

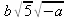
> simplify(GAMMA(n+1)/n!);

Действие функции simplify существенно зависит от областей определения переменных. В следующем примере упрощение выражения не произошло, поскольку результат этой операции неоднозначен: