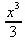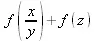Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Для более детального анализа объектов может использоваться функция hastype(expr, t), где expr — любое выражение и t — наименование типа подобъекта.

Эта функция возвращает логическое значение true, если подобъект указанного типа содержится в выражении expr. Примеры применения этой функции даны ниже (файл control):

> hastype(2+3,integer);

> hastype(2+3/4,integer);

> hastype(2*sin(x),function);

> hastype(a+b-c/d,`+`);

Еще одна функция — has(f,x) — возвращает логическое значение true, если подобъект х содержится в объекте f, и false в ином случае:

> has(2*sin(х),2);

> has(2*sin(x), `/`);

> has(2*sin(x),3-1);

Следует отметить, что соответствие подобъекта выражения указанному подобъекту понимается в математическом смысле. Так, в последнем примере подобъект «3-1», если понимать его буквально, в выражении 2*sin(x) не содержится, но Maple-язык учитывает соответствие 3-1=2, и потому функция has в последнем примере возвращает true.

Функция has может использоваться для выявления той или иной математической операции, оператора или функции. Однако надо соблюдать определенные правила, поскольку выражение, анализируемое функцией has оценивается и исполняется. Внимательно проанализируете приведенные ниже примеры:

> has(2*sin(2),sin);

> has(2*sin(2),'sin');

> has(2*sin(2.), 'sin');

Здесь надо учесть, что выражение 2*sin(2) после оценки и исполнения не меняется, поскольку Maple, при целочисленном аргументе функции синуса, не вычисляет ее и вычисленное выражение совпадает с исходным и содержит функцию синуса. Однако sin(2.) уже вычисляется и становится числом. Именно поэтому в последнем примере функция sin уже не обнаруживается. Подобное имеет место и в ряде других примеров с функцией интегрирования:

> has('int(х^2,х)',int);

> has(int(х^2,х),int);

> int(х^2,х);

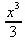
> has(int(х^2,х), х^3/3);rue

Столь же поучителен пример с идентификацией функции интегрирования. Так, has(int(х^2, х), int); дает false, поскольку интеграл оценивается и вычисляется, что ведет к подмене выражения на х^3/3 уже не содержащего признаков интегрирования. Это и поясняют два последних примера, в которых вычислено значение интеграла и функция has дает значение true для значения интеграла. В тоже время заключение int(x^2,x) в апострофы позволяет найти имя функции интегрирования int, поскольку исходное выражение в этом случае представлено в неисполняемой форме и содержит обращение к этой функции.

Еще одна иногда полезная функция контроля выражений depends(f,x) возвращает true, если х входит в f и false в противном случае. При этом надо также помнить, что функция (выражение) оценивается и исполняется. Следующие примеры хорошо иллюстрируют сказанное:

> depends(2+2*sin(x),х);

> depends(int(х^2,х),х);

> depends(int(х^2,х=0..1), х)

В последнем примере вычисленное выражение это уже просто число, в нем х не содержится, а потому и получено значение false.

Нередко бывает необходимо заменить некоторое подвыражение в заданном выражении на функцию от этого подвыражения, т.е. осуществить подстановку. Средства для обеспечения подстановок есть во всех СКМ. Так, для этого в Maple 9.5 можно воспользоваться функцией applyop:

• applyop(f, i, е) — применяет функцию f к i-му подвыражению выражения е;

• applyop(f, i, е…, xk,…) — применяет функцию f к i-му подвыражению выражения е с передачей необязательных дополнительных аргументов xk.

Ниже даны примеры применения этой функции (здесь и далее см. файл subs):

> restart;applyop(sin,2,a+x);

> applyop(f,1,g,2,a+b);

> applyop(f,{2,3},a+x+b);

> applyop(f,{1,2},x/y+z);

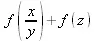
> р:=у^2-2*у-3;

> applyop (f, 2,p);

> applyop{f,[2, 3 ], p);

> applyop(f,{[2,1],3},p);

> applyop(abs,{[2,1],3},p);

Еще две функции, реализующие операции подстановки, указаны ниже: