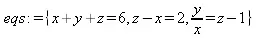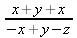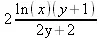Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Одним из важных применений подстановок является проверка правильности решений уравнений и систем уравнений. Ниже дан пример такой проверки:

> eqs:={x+y+z=6,y/x=z-1,z-x=2};

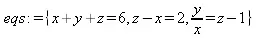
> res:=solve(eqs,{х,у,z});

> subs(res,eqs);

> subs(c=a-b,(а^2-2*а*b+b^2)/с);

Здесь задана система из трех нелинейных уравнений, которая затем решена функцией solve. В конце примера с помощью функции подстановки выполнена проверка правильности решения. Оно верно, поскольку у всех уравнений значение левой части совпадает со значением правой части.

Для применения некоторого правила или списка правил rule к некоторому выражению expr используется функция applyrule(rule, expr). Применение этой функции достаточно очевидно:

> restart:applyrule(f(а::integer*х)=a*f(х),f(2*х)+g(х)-p*f(х));

> applyrule(х^2=у,f(x^2,ln(cos(x)+2*x^2)));

> applyrule(b+c=x,f(a+b+c+d));

Эта функция более мощная, чем subs, но она не выполняет математические вычисления, подобно тому, как это делает функция algsubs(a=b, f, v, options) с необязательными двумя последними параметрами. Проанализируйте следующие примеры

> algsubs(а^2=0, ехр(2-а+а^2/2-а^3/6));

> applyrule(а^2=0, ехр(2-a+a^2/2-a^3/6));

и различия между этими функциями подстановки станет ясным.

Сортировка и селекция выражений широко используются в практике символьных преобразований. Нередко она важна в статистических расчетах, обеспечивая повышение их точности.

Для выполнения сортировки служит функция sort, применяемая в одной из следующих форм:

sort(L)

sort(L, F)

sort(A)

sort(A, V)

Здесь L — список сортируемых значений, F — необязательная булева процедура с двумя аргументами, А — алгебраическое выражение, V — необязательные дополнительные переменные.

Примеры применения этих функций (файл sortsel)

> restart;

> sort([у, s,f,a,c,i] ); t([2,5,1,7,3,8]);

> sort([y,s,f,a,c,i]);

> sort([у,s,f,а,с,i],lexorder);

> sort(1+х^4-х^2+х);

> sort(у*х^2+х*у+у-х^2+х^4*у^5);

> sort((y+z+x)/(y-x-z),{x, y});

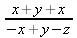
> names:= ["Peter","Anna","Vladimir", "Ivan"];

> sort(names);

> integers:=[$10..30];

Если функция сортировки меняет порядок расположения членов в выражении (или порядок расположения выражений), то другая функция — select — служит для выделения требуемого выражения:

select(f, е)

select(f, е, b1, ..., bn)

Как бы обратной ей по действию служит функция remove, устраняющая заданные выражения:

remove(f, е)

remove(f, е, b1,.... bn)

В этих функциях f — процедура, возвращающая логическое значение, е — список, множество, сумма, произведение или функция, b1, …, bn — необязательные дополнительные аргументы.

Ниже даны примеры применения этих функций (файл sortsel):

> integers := [$10..30]:

> select(isprime,integers);

> remove(isprime,integers);

> f:=2*ln(a*x)*exp(x)*ln(y);

> select(has,f,x);

> remove(has,f,x);

> f:=indets(f);

> select(type,f,name);

> remove(type,f,name);

> f:=2*ln(x)*(y+1);

> c:=remove(has,f,x);

> f/c;

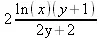
> select(has,f,x);

Maple имеет также оператор селекции А[expr]. Его действие поясняют следующие примеры (файл sortsel):

> restart;

> S:=[a+b*c,х^2,с,1,2,3];

> S[1];

> S[1..2];

> S[-2..-1];

> S[3..3];

> S[3..2];

> S[4..6];

> X:=S[];