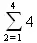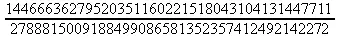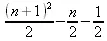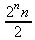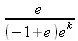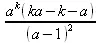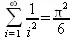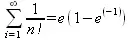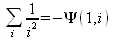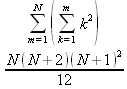Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

sum(f,k);

sum(f,k=m..n);

sum(f,k=alpha);

Sum(f,k);

Sum(f,k=m..n);

Sum(f,k=alpha).

Здесь f — функция, задающая члены суммируемого ряда, k — индекс суммирования, тип — целочисленные пределы изменения k, alpha — RootOf-выражение. Значение n может быть равно бесконечности. В этом случае для n используется обозначение ∞ или infinity. Допустимо (а зачастую рекомендуется с целью исключения преждевременной оценки суммы) заключение f и k в прямые кавычки — например, sum('f', 'k'=m..n). Рекомендуется все примеры проверять после команды restart, убирающей предыдущие определения f и k.

Внимание! При вычислении сумм (и произведений) последовательностей надо строго соблюдать прямой (нарастающий) порядок задания значений индексной переменной суммы. Нарушение этого порядка чревато грубыми ошибками. Так что правила о том, что при измени порядка суммируемых или умножаемых членов последовательности сумма и произведения не меняются в данном случае не поддерживаются на программном уровне.

Простейшими являются суммы последовательностей с фиксированным числом членов. Ниже даны примеры применения этих функций (файл sum):

> restart;k:=2;

> Sum(k^2,k=1..4);

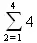
> sum(k^2,k=1..4);

Error, (in sum) summation variable previously assigned, second argument evaluates to k=1..4

> sum('k^2','k'=1..4);

> sum(1/i,i=1..100);

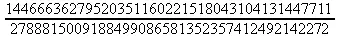
> evalf(%);

Обратите внимание, что во втором примере система отказалась от вычисления, а в третьем даже выдала сообщение об ошибке, связанную с тем, что переменной k перед вычислением сумм было присвоено численное значение 2. После заключения выражения и переменной индекса k в прямые кавычки ошибка исчезла, поскольку такая операция означает, что переменной придается неопределенное значение.

Особый класс образуют последовательности, у которых существует их предел в аналитическом виде. Ниже представлен ряд последовательностей, у которых переменная индекса задается как 0..n или 1..n (файл sum):

> restart;

> sum(k, k=1..n);

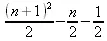
> sum(i/(i+1),i=0..n);

> sum(k*binomial(n,k),k=0..n);

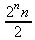
Некоторые из таких сумм выражаются через специальные математические функции.

Многие суммы бесконечных рядов сходятся к определенным численным или символьным значениям, и система Maple способна их вычислять. Это поясняют следующие примеры (файл sum):

> restart;

> sum(-exp(-k), k);

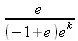
> sum(k*a^k,k);

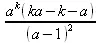
> sum(1/k!,k=0..infinity);

> Sum(1/i^2, i=1..infinity) = sum(1/i^2, i=1..infinity);

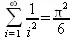
> Sum(1/n!, n=1..infinity) = sum(1/n!, n=1..infinity);

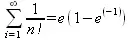
> evalf(%);

> Sum(1/i^2, i)=sum(1/i^2, i);

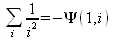
Могут встречаться множественные суммы по типу «сумма в сумме». Ограничимся приведением примера двойной суммы, имеющей аналитическое значение (файл sum):

> Sum(Sum(k^2, k = 1..m), m = 1..N); factor(simplify(value(%)));

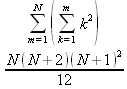
При конкретном значении N такую сумму нетрудно вычислить подстановкой:

> subs(N = 100, %);

Как видно из приведенных примеров, средства вычисления сумм последовательностей Maple 9.5/10 позволяют получать как численные, так и аналитические значения сумм, в том числе представляемые специальными математическими функциями.

Возможности вычисления специальных сумм существенно расширяются при использовании инструментального пакета вычисления специальных сумм sumtools. При его вызове выводится список функций пакета: