Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

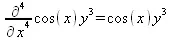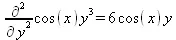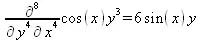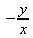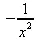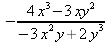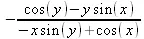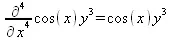
> Diff(f(х,у),y$2)=diff(f(х,у), у$2);

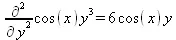
> Diff(f(х,у), х$4,у$4)=diff(f(х,у),х$3,у$2);

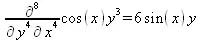
Получаемые в результате дифференцирования выражения могут входить в другие выражения. Можно задавать их как функции пользователя и строить графики производных.

Для создания функций с производными может также использоваться дифференциальный оператор D. Порою он позволяет создавать более компактные выражения, чем функции diff и Diff. Дифференциальный оператор можно записывать в следующих формах: D(f) или D[i](f), где параметр f — выражение или имя функции, i — положительное целое число, выражение или последовательность. Оператор D(f) просто вычисляет имя производной от f, поскольку в этой форме он эквивалентен unnaply(diff(f(x),x),x). В форме D(f)(x) этот оператор подобен diff(f(x),x).

Приведем примеры дифференцирования функций, заданных только именами, и функций с одним параметром (файл D):

> restart;

> D(cos^2);

> D(exp^2+cos^2+tan+GAMMA);

> D(sin)(x)=diff(sin(x), x);

> D[1](sin*cos);

Следующий пример показывает дифференцирование функции пользователя fun с применением дифференциального оператора D и функции diff:

> fun:=(x)->sin(x^2);

> D(fun)=diff(fun(x),x);

Дифференциальный оператор можно применять и для дифференцирования функций нескольких переменных по заданной переменной (файл D):

> f := (х, у, z)->х*ехр(у)+ln(z);

> D[1](f);

> D[2](f);

> D[3](f);

Пример применения дифференциального оператора для функции f, заданной программным объектом-процедурой, представлен ниже:

> restart;

> f:=proc(x,b,n) local i,d,s;

> s:=0;

> for i from n by -1 to 0 do s:=s*x+b[i] od;

> s

> end:

-> D[1](f);

proc(x, b, n)

local i, s, sx;

sx := 0;

s := 0;

for i from n by -1 to 0 dosx

sx := sx×x + s;

s := sx×x + b[i]

end do;

sx

end proc

Этот пример показывает реализацию схемы Горнера для полинома b степени n от переменной х. При этом применение оператора дифференцирования возвращает процедуру. Ряд интересных возможностей по вычислению производных предоставляет пакет расширения student.

Иногда подлежащая дифференцированию зависимость задана импликативно, т.е. в виде уравнения f. Для дифференцирования таких зависимостей служит функция, используемая в виде:

implicitdiff(f,у,х)

implicitdiff(f,у,x1,...,xk)

Примеры применения импликативного дифференцирования приведены ниже (файл impldiff):

> f1 := х*у=1:implicitdiff(f1, у, x);

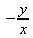
> subs(y=1/x,%);

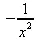
> f2:=2*х^4-3*х^2*у^2+у^4=16:implicitdiff(f2, у, х);

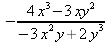
> f3:=x*cos(у)+y*cos(х)=1:implicitdiff(f3,у,x);

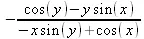
В справке по этой функции можно найти более сложные формы записи этой функции и дополнительные примеры ее применения.

При обучении основам математического анализа удобны обучающие средства на основе Maplet-технологии. Эти новые средства (их не было даже в Maple 9) размещены в позиции Tools меню системы Maple 9.5 при ее применении в стандартном виде. Команда Tools→Tutors Calculus-Single Variables→Derivatives… открывает окно Maple-вычислителя производных, показанное на рис. 4.1.

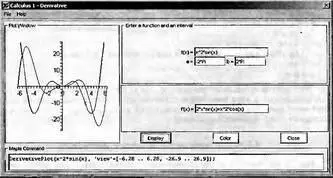
Рис. 4.1 Окно Maplet-вычислителя производных

В окне можно в интерактивном режиме задать выражение для функции f(x), вычислить производную f'(x) и, нажав кнопку Dispay, получить графики заданной функции и ее производной в заданных пределах изменения х от а до b. При закрытии окна графики появляются в текущей строке вывода системы Maple 9.5.