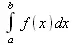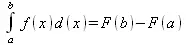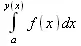Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

При изучении раздела производных в курсе математического анализа особое значение имеют навыки учащегося в пошаговом дифференцировании выражений в аналитическом виде. В то время, как инженера или научного работника часто удовлетворяет конечное выражение при дифференцировании заданного выражения, учащегося не в меньшей (а порою в куда большей) мере интересуют детали промежуточных вычислений.

Такую возможность обеспечивает инструмент Differentiate Methods… по методам аналитического дифференцирования производных. Для открытия его окна надо исполнить команду Tools→Tutors Calculus-Single Variables→Differentiate Methods…. Это окно показано на рис. 4.2.

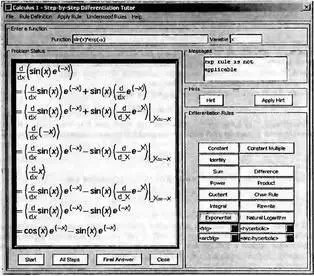
Рис. 4.2. Окно Maplet-инструмента по методам дифференцирования

Окно имеет свое меню, область задания функции Function заданной переменной, область вывода функции и результатов ее преобразований и область с кнопками, позволяющими задавать правила дифференцирования и наблюдать результаты их выполнения. Можно задать выполнение всех шагов дифференцирования сразу по всем шагам (кнопка All Steps) или запустить дифференцирование раздельно по шагам (кнопка Start).

С помощью кнопки Hint можно вызвать советы по дифференцированию и применить их активизацией кнопки Apply Hint. В поле Differentiate Rules (Правила дифференцирования) имеется множество кнопок, позволяющих применить те или иные правила дифференцирования заданного выражения и опробовать их эффективность. Таким образом имеется возможность выполнить дифференцирование в аналитическом виде различными методами, задаваемыми пользователем. Пример на рис. 4.2 показывает дифференцирование функции f(x)=sin(x)*exp(-х). Представлены шаги дифференцирования и конечный результат.

Интегральное исчисление зародилось из практической необходимости вычисления площадей, объемов и центров тяжести различных фигур. Если есть некоторая функция f(х), то определенный интеграл вида

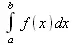
дает значение площади, ограниченной вертикалями а и именуемыми пределами интегрирования, кривой f(х) и осью абсцисс X. Под площадью надо понимать ее алгебраическое значение, то есть разность между площадью над осью X и под ней. В этом случае ясно, что определенный интеграл может иметь как положительные, так и отрицательные значения.

Если f(x)dx есть дифференциал функции F(x), то

Функцию F(x) называют первообразной функции f(х). Наиболее общий вид первообразной функции f(x) называют неопределенным интегралом и обозначают как

Соответственно определенный интеграл определяется как:

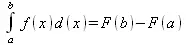
В состав этого выражения включена некоторая постоянная интегрирования С, подчеркивающая, что для одной и той же f(х) существует масса первообразных, описываемых одной и той же линией, но смещенных по вертикали на произвольную постоянную. Например, для f(х)=sin(x) имеем

Определенный интеграл представляется числом, а неопределенный — функцией. Для их вычисления используются принципиально различные методы. Так, вычисление неопределенного интеграла возможно только в системах символьной математики. А вот для вычисления определенных интегралов используются как символьные, так и численные методы интегрирования.

Встречается ряд специальных видов интегралов. Один из них — интеграл с переменным верхним пределом, представленный в виде:

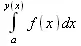
В данном случае верхний предел представлен функцией y(х).

Следует отметить, что Maple обычно стремиться вычислить определенный интеграл в аналитическом виде, даже если он представляется числом. Если нужно найти заведомо численное значение определенного интеграла, можно воспользоваться численными методами вычисления.

Для вычисления неопределенных и определенных интегралов Maple предоставляет следующие функции:

int(f,x); int(f,х=а..b);

int(f,х=а..b,continuous);