Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

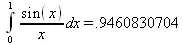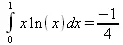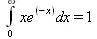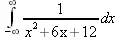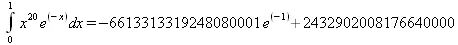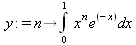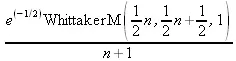
> Int(х*ln(х),х=0..1)=int(x*ln(x), х=0..1);

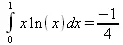
> Int(х*ехр(-х),х=0..infinity)=int(х*ехр(-х), х=0..infinity);

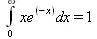
> Int(1/(х^2+6*х+12),x=-infinity..infinity);

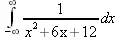
> value(%);

Как видно из этих примеров, среди значений пределов может быть бесконечность, обозначаемая как infinity.

Рассмотрим интеграл, который встречает трудности при вычислении с ограниченным числом верных знаков в процессе вычислений. Maple 8/9/9.5 (кстати, как и Mathematica 4/5), с легкостью берут этот интеграл и позволяют сразу и без какой-либо настройки вычислить для него как точное, так и приближенное значение:

> Int(х^20*ехр(-х),х=0..1)=int(х^20*ехр(-х),х=0..1);

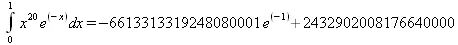
> evalf(%,30);

Любопытно, что версия Maple 6 при задании погрешности по умолчанию вычисляла значение этого интеграла также как 0, тогда как Maple 9.5 «поумнел» уже настолько, что дает значение 0.01835046770 даже в этом, не очень удачном, случае. Более того Maple 9/9.5 позволяет наглядно проиллюстрировать характер промежуточных вычислений подобных интегралов:

> int(х^20*ехр(-х),х);

Нетрудно заметить, что решение распадается на множество слагаемых, соответствующих общеизвестному интегрированию по частям. В каждом слагаемом имеются большие числа и потому принципиально необходимо применение арифметики высокой точности (или разрядности). Maple 9/9.5 такими средствами, причем превосходными, обладает.

Продолжим изучение данного «каверзного» интеграла. Опробуем силы Maple на интеграле более общего вида, где конкретный показатель степени заменен на обобщенный — n. Здесь нас ожидает приятный сюрприз — Maple с легкостью выдает аналитическое решение для данного определенного интеграла:

> у:=(n)->int(х^n*ехр(-х),х=0..1);

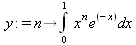
> y(n);

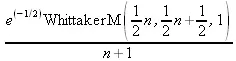
> y(20);

> evalf(%,30);

> у(20.);

Однако радоваться несколько преждевременно. Многие ли знают, что это за специальная функция — WhittakerM? Но хуже другое — Maple при конкретном n=20 дает грубо неверное решение — 0 (почему — уже объяснялось). Забавно, что при этом сама по себе функция WhittakerM вычисляется для n=20 без проблем:

> WhittakerM(10,10.5,1);

А теперь присмотритесь к новому результату вычисления злополучного интеграла. Оказывается, он уже не содержит больших чисел, свойственных прямому решению! Зная значение WhittakerM с погрешностью по умолчанию, можно уверенно вычислить приближенное численное значение интеграла с той же погрешностью, уже не прибегая к арифметике высокой точности:

> (ехр(-.5)*WhittakerM(10,10.5,1))/21;

На рис. 4.3 приведен график зависимости значений данного интеграла от показателя степени n при его изменении от 0 до 50. Плавный ход графика показывает, что в вычислении данного интеграла нет никаких признаков неустойчивости решения при изменении n, если соблюдать правило выбора достаточно малой погрешности вычислений.

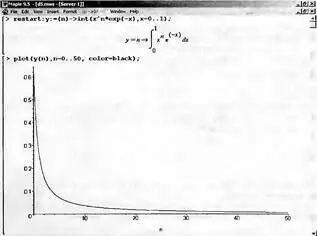
Рис. 4.3. Значение интеграла от х^nехр(-х) как функция n

Наличие у функции особых (сингулярных) точек нередко затрудняет выполнение с ней ряда операций, таких как численное интегрирование. В этом случае могут помочь соответствующие параметры. Например, вычисление в Maple 8/9 следующего интеграла дает явно неудобное выражение в виде набора значений, разных для разных интервалов изменения a:

> int(1/(х+а)^2,х=0..2);

Этот интеграл расходится, поскольку при x=-a подынтегральная функция устремляется в бесконечность, что и показывает приведенное выражение. График зависимости значения интеграла от параметра а имеет подозрительный вид.