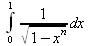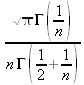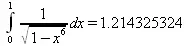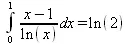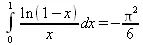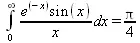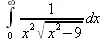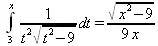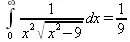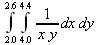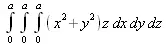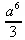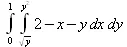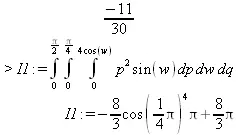Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

> Int(1/sqrt(1-х^n),х=0..1);

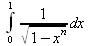
> value(%);

Definite integration: Can't determine if the integral is convergent. Need to know the sign of —> n

Will now try indefinite integration and then take limits.

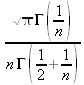
> Int(1/sqrt(1-х^6),х=0..1)=evalf(int(1/sqrt(1-х^6) , х=0..1));

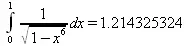
Приведем тройку примеров, требующих для вычислений «вручную» заметных умственных усилий, но прекрасно выполняемых системой Maple:

> Int((х-1)/ln(х),х=0..1)=int((х-1)/ln(х),х=0..1);

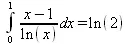
> Int(ln(1-х)/x,x=0..1)=int(ln(1-х)/x,x=0..1);

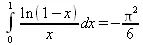
> Int(exp(-x)*sin(x)/x,x=0..infinity)=int(exp(-x)*sin(x)/x, x=0..infinity);

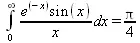
Однако не стоит думать, что всегда «коту масленица». Следующий интеграл дает весьма подозрительный результат:

> Int(1/(х^2*(sqrt(х^2-9))),х=0..infinity);

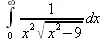
> value(%);

Это наглядный пример, когда Maple 9.5 «нагло врет», несмотря на заверения его создателей о том, что эта система прошла полную сертификацию на вычисления интегралов. Выполнив некоторые преобразования, найдем интеграл в системе Maple 8:

> Int(1/(t^2*(sqrt(t^2-9))), t=3..x) = int(1/(t^2*(sqrt(t^2-9))), t=3..x);

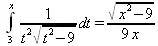
Увы, Maple 9.5 вычислять данный интеграл не желает — он его просто повторяет. Но, и в Maple 8 и в Maple 9.5 нужное значение определяется пределом этого выражения при х, стремящемся к бесконечности:

> Int(1/(x^2*(sqrt(х^2-9))),х=0..infinity) = value(Limit(rhs(%),x=infinity));

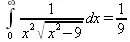
Этот пример наглядно показывает, что иногда полезны аналитические преобразования, выполняемые «вручную», то бишь с помощью своей головы. К сожалению, с подобными «фокусами» иногда приходится встречаться.

Приведенные примеры говорят о том, что и новые реализации Maple не лишены отдельных недостатков, возможно и привнесенных в их доработанное ядро. В общем, как говорят у нас в армии «Доверяй, но — проверяй!». Интегралы, представляемые через специальные математические функции, Maple 9.5/10 нередко вычисляет хуже, чем система Mathematica 4.5/5.

К интересному классу интегралов относятся определенные интегралы с переменными пределами интегрирования. Если обычный определенный интеграл представлен числом (или площадью в геометрической интерпретации), то интегралы с переменными пределами являются функциями этих пределов.

На рис. 4.8 показано два примера задания простых определенных интегралов с переменным верхним пределом (сверху) и обоими пределами интегрирования (снизу).

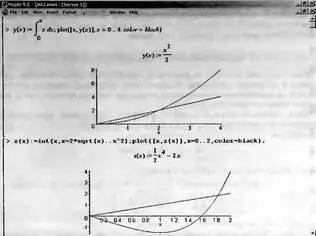
Рис. 4.8. Примеры интегралов с переменными пределами интегрирования

На этом рисунке построены также графики подынтегральной функции (это наклонная прямая) и функции, которую задаёт интеграл.

Функции int и Int могут использоваться для вычисления кратных интегралов, например, двойных и тройных. Для этого функции записываются многократно (файл intm):

> restart;

> Int(int(1/(x*y),x=4.0..4.4),y=2.0..2.6);

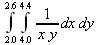
> value(%);

> Int(Int(Int((х^2+у^2)*z, x=0..a), y=0..a), z=0..a);

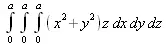
> value(%);

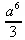
> Int(Int(2-х-у, x=sqrt(у)..у^2), у=0..1);

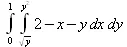
> value(%);

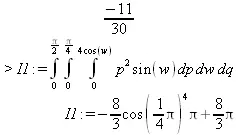
> evalf(I1);

Обратите внимание на нечеткую работу функции evalf в последнем примере. Эта функция уверенно выдает значение evalf(Pi) в форме вещественного числа с плавающей точкой, но отказывается вычислить значение интеграла, в которое входит число Pi. Этот пример говорит о том, что отдельные недостатки у Maple все же есть, как и поводы для ее дальнейшего совершенствования. В пакете расширения student имеются дополнительные функции интегрирования, которые дополняют уже описанные возможности. В частности, в этом пакете есть функции для вычисления двойных и тройных интегралов.