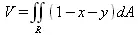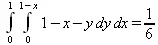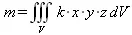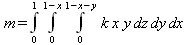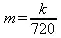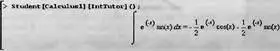Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Maple открывает большие возможности в вычислении криволинейных, поверхностных и объемных интегралов. Нередко такие интегралы довольно просто заменяются на интегралы с переменными пределами интегрирования, что и иллюстрируют приведенные ниже примеры.

Пусть требуется вычислить объем фигуры, ограниченной координатными плоскостями и плоскостью х+ у + z= 1. Он, с учетом равенства z= 1-х-у, задается интегралом:

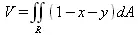
который заменяется следующим интегралом:

> Int(Int(1-х-у,у=0..1-х),х=0..1)=int(int(1-х-у,у=0..1-х),х=0..1);

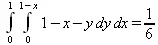
Последний, как видно, легко вычисляется.

Теперь вычислим массу указанной фигуры, которая задается тройным интегралом:

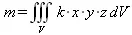
Здесь k — константа, характеризующая удельную площадь вещества. Этот интеграл также сводится к легко решаемому в Maple 9.5:

> m=Int(Int(Int(k*x*y*z,z=0..1-x-y),y=0..1-х),x=0..1);

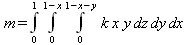
> value(%);

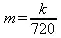
Специальные средства для вычисления подобных интегралов имеет пакет расширения VectorCalculus, который описывается в конце этой главы.

В составе самоучителей Maple 9.5 есть раздел Antiderivative, который иллюстрирует технику построения первообразной функции при интегрировании. Для доступа к окну этого инструмента (рис. 4.9) достаточно исполнить команду Tools→Tutors→Calculus-Single Variables→Antiderivative….

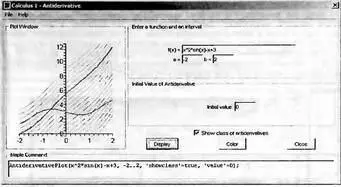
Рис. 4.9. Окно Maplet-демонстрации графиков функций и первообразных

Окно Maplet-демонстрэции интегрирования позволяет задать подынтегральную функцию и построить ее график и график первообразной функции, представляющей неопределенный интеграл. В окне а и b это не пределы интегрирования, а пределы изменения х при построении графиков. Опция Show class of antiderivatives позволяет построить графики множества первообразных, с выделением графика первообразной функции для заданного начального значения Initial Value. По завершении работы с окном демонстрации графики выводятся в документ Maple 9.5 — рис. 4.10.

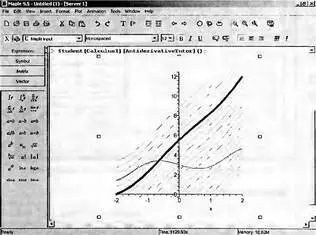
Рис. 4.10. Графики исходной функции и первообразных в окне документа Maple 9 5

Для демонстрации методов пошагового интегрирования имеется Maplet-инст-румент Step-by-step Integration Tutor. Для вызова его окна (рис. 4.11) нужно исполнить команду (в стандартном варианте интерфейса): Tools→Tutors→Calculus-Single Variables→Antiderivative….

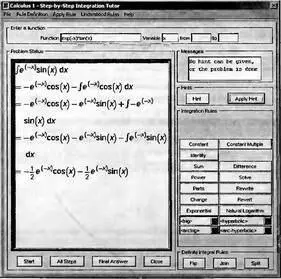
Рис. 4.11. Окно Maplet-демонстрации методов пошагового интегрирования

Нетрудно заметить, что это окно практически аналогично окну для демонстрации методов пошагового дифференцирования, описанному в разделе 4.3.4 (рис. 4.2). В связи с этим подробное описание средств этого инструмента можно опустить. Отметим лишь, что он позволяет задавать подынтегральную функцию и пределы интегрирования и по шагам (автоматически или вручную) вычислять интегралы. По окончании работы с окном соответствующий интеграл и результат его вычисления появляется в окне документа — рис. 4.12.

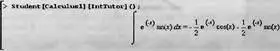
Рис. 4.12. Пример вывода результата работы с Maplet-инструментом по методам интегрирования

Для численного вычисления определенных интегралов используется функция evalf в сочетании с функциями Int или int:

evalf(Int(f, x=a..b, …))

evalf(Int(f, a..b, …))

evalf(Int(f, list-of-equations, …))

evalf(Int(f, list-of-ranges, …))

evalf(int(f, x=a..b))

Вместо многоточия могут использоваться различные опции, например, для задания метода вычислений. Могут использоваться комбинированные методы (аналитический с численным), ряд Maple-методов повышенной точности, методы предложенные группой NAG, метод Монте-Карло и др. Детали задания методов можно найти в справке. Ограничимся несколькими примерами вычисления определенных интегралов в численном виде (файл intnum):