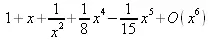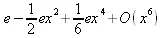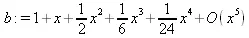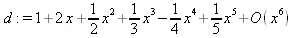В выражении expr могут использоваться операторы +, -, *, / и ^. С ними могут комбинироваться встроенные функции и функции пользователя, например fig). Кроме того, могут использоваться следующие функции:
Powexp powinv powlog povmeg powrev
Powdiff powint powquo powsub powcos
Powtan powsec powcsc powcot powsinh
Powcosh powtanh powsech powcsch powcoth
Powsqrt powadd multiply
4.6.6. Примеры выполнения степенных разложений
Назначение большинства этих функций очевидно из их названий — они возвращают соответствующую функцию (указанную после слова pow в имени) в виде разложения в ряд или полинома. Например, powexp раскладывает выражения с экспоненциальными функциями в ряд.
Получаемые функциями ряды представляются в специальном формате. Поэтому для их применения в обычном виде необходимо использовать функцию tpsform в следующих видах:
tpsform(p, var, order) — преобразует ряд p в обычную форму с заданием порядка order;
tpsform(p, var) — преобразует ряд p в обычную форму с порядком, заданным переменной Order.
Здесь p — имя степенного ряда, var — переменная, относительно которой записан ряд, order — порядок ряда. Если параметр order не указан, используется значение глобальной переменной Order. Ниже даны примеры, иллюстрирующие технику работы со степенными разложениями (файл pseries):
> p1:=powexp(sin(х));
p1:= proc(powparm) … end proc
> p2:=powexp(cos(x));
p2 := proc(powparm) … end proc
> tpsform(p1,x);
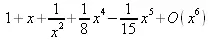
> tpsform(p2,x);
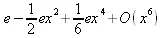
> a := powseries[powexp](x):
> b := powseries[tpsform](a, x, 5);
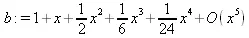
> с := powadd(powpoly(1+x^2+x,x), powlog(1+x)):
> d := tpsform(c, x, 6);
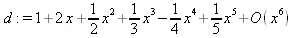
4.6.7. Maplet-иллюстрэция аппроксимации рядом Тейлора в ряд
Для демонстрации разложения аналитической функции в ряд имеется Maplet-инструмент Taylor Approximation. Для вызова его окна (рис. 4.19) нужно исполнить команду (в стандартном варианте интерфейса): Tools→Tutors→Calculus-Single Variables→Taylor Approximation….
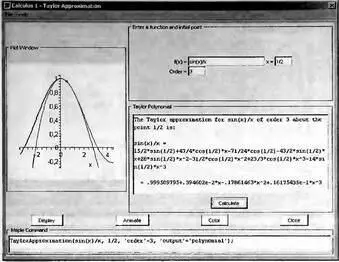
Рис. 4.19. Окно Maplet-демонстрации аппроксимации функции рядом Тейлора
Нетрудно заметить, что это окно практически аналогично окну для демонстрации методов пошагового дифференцирования, описанному в разделе 4.3.4 (рис. 4.2). В связи с этим подробное описание средств и этого инструмента можно опустить. Отметим лишь, что он позволяет задавать функцию и значение x в точке разложения. По окончании работы с окном соответствующий предел и результат его вычисления появляется в окне документа. Можно просматривать постепенное улучшение приближения по мере увеличения порядка метода в режиме анимации.
4.7. Визуализация приложений математического анализа
Любая СКМ имеет возможности для визуализации различных приложений математического анализа. Особое внимание этому уделено в системе Maple 9.5, где с помощью Maplet-средств созданы самоучители, обеспечивающие наглядное представление приложений математического анализа.
4.7.1. Суммы Римана и приближение интегралов
Есть два основных способа вычисления определенных интегралов в численном виде:
• на основе сумм Римана (варианты метода прямоугольников);
• на основе приближения подынтегральной функции той или иной зависимостью.
Оба метода реализуются Maplet-инструментом Approximate Integration. Для вызова окна этого инструмента (рис. 4.20) нужно исполнить команду (в стандартном варианте интерфейса): Tools Tutors→Calculus-Single Variables→Approximate Integration…. Совершенно аналогичное окно выводит команда Tools→Tutors→Calculus-Single Variables→Rieman summs….
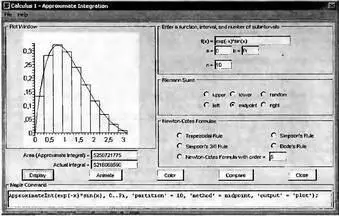
Рис. 4.20. Пример приближения интеграла суммой Римана (10 прямоугольников с центральным расположением)
В правой части окна размещены панели:
• ввода функции f(х), пределов а и b и числа интервалов разбиения
• задания расположения прямоугольников, которые образуют сумму Римана;
• методов Ньютона-Котеса;
Относительно каждой ординаты прямоугольник может быть ориентирован сверху или снизу, справа или слева, посередине или даже случайным образом. При реализации формул приближения Ньютона-Котеса возможно применение метода трапеций, двух вариантов метода Симпсона (квадратичное приближение), метода Боде и известных формул Ньютона-Котеса заданного порядка (по умолчанию 5). В функциях численного интегрирования Maple тот или иной вид приближения можно задать явно, но по умолчанию метод выбирается автоматически. После выбора метода можно получить его графическую иллюстрацию (рис. 4.20), нажав мышью кнопку Display.
Читать дальше
Конец ознакомительного отрывка
Купить книгу