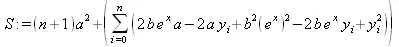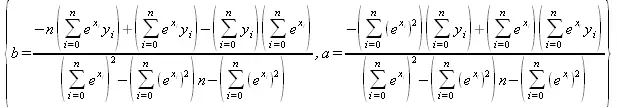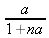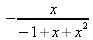Maple позволяет решать уравнения с линейными операторами, например, с операторами суммирования рядов и дифференцирования. Ограничимся одним примером такого рода (файл solvefo):
> S := sum((a+b*exp(x[i])-y[i])^2, i=0..n);
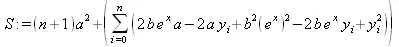
> eqns := {diff(S, a), diff(S,b)};
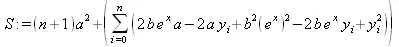
> solve(eqns, {a, b});
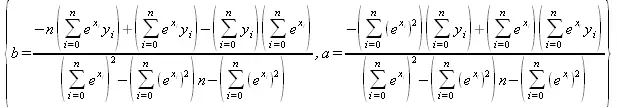
4.8.11. Решение в численном виде — функция fsolve
Для получения численного решения нелинейного уравнения или системы нелинейных уравнений в формате вещественных чисел удобно использовать функцию
fsolve(eqns, vars, options)
Эта функция может быть использована со следующими параметрами:
complex — находит один или все корни полинома в комплексной форме; fulldigits — задает вычисления для полного числа цифр, заданного функцией Digits;
maxsols=n — задает нахождение только n корней;
interval — задается в виде а..b или х=а..b или {x=a..b, y=c..d, …} и обеспечивает поиск корней в указанном интервале.
Функция fsolve дает решения сразу в форме вещественных или комплексных чисел, что и показывают следующие примеры (файл fsolve):
> fsolve(sin(х)=Pi/4,х);
.9033391108
> fsolve(sin(х)=1/2,х=4..8);
6.806784083
> fsolve(2*х^2+х-1=10,x);
-2.608495283, 2.108495283
> fsolve(х^5-х,x);
-1., 0., 1.000000000
> fsolve(х^5-х,x,complex);
-1.000000000, -1.000000000 I, 0., 1.000000000 I, 1.000000000
> eqns := abs(x)*x+exp(x) > 0;
eqns:= 0 <|x|x +e x
> solve(eqns, {x});
{-2 LambertW(½)
> f := sin(x+y) — exp(x)*y = 0: g := x^2 - у = 2:
fsolve{{f,g},{x,y},{x=-1..1,y=-2..0});
{x = -.6687012050, у = -1.552838968}
Заметим, что локализация поиска корней в заданном интервале позволяет отыскивать такие решения, которые не удается получить с помощью функций solve и fsolve в обычном применении. В последнем из приведенных примеров дается решение системы нелинейных уравнений, представленных уравнениями f и g.
Чтобы еще раз показать различие между функциями solve и fsolve, рассмотрим пример решения с их помощью одного и того же уравнения erf(x) = 1/2:
> solve(erf(х)=1/2,х);
RootOf(2 erf(_Z) -1)
> fsolve(erf(x)=1/2);
.4769362762
Функция solve в этом случае находит нетривиальное решение в комплексной форме через функцию RootOf, тогда как функция fsolve наводит обычное приближенное решение.
Мы уже отмечали, что функция solve дает решение уравнения ехр(-х) = х в форме специальной функции Ламберта. Нетрудно заметить, что функция fsolve дает результат сразу в форме числа с плавающей точкой:
> restart;eq:=exp(-х)=х;sol:=fsolve(ехр(-х)=х,х);
eq: = e (-x)= х
sol: =0.5671432904
4.8.12. Решение рекуррентных уравнений — rsolve
Функция solve имеет ряд родственных функций. Одну из таких функций — fsolve — мы рассмотрели выше. В справочной системе Maple можно найти ряд и других функций, например rsolve для решения рекуррентных уравнений, isolve для решения целочисленных уравнений, msolve для решения по модулю m и т.д. Здесь мы рассмотрим решение уравнений важного класса — рекуррентных. Напомним, что это такие уравнения, у которых заданный шаг решения находится по одному или нескольким предшествующим шагам.
Для решения рекуррентных уравнений используется функция rsolve:
rsolve(eqns, fens)
rsolve{eqns, fens, 'genfunc'(z))
rsolve(eqns, fens, 'makeproc')
Здесь eqns — одиночное уравнение или система уравнений, fens — функция, имя функции или множество имен функций, z — имя, генерирующее функциональную переменную.
Ниже представлены примеры применения функции rsolve (файл rsolve):
> restart;
> rsolve(f(n)=-2*f(n-1)-f(n-2), f(k));
(-f(0) -f(1))(k + 1)(-1) k+(f(1) +2f(0))(-1) k
> rsolve({f(n)=-3*f(n-1)-2*f(n-2),f(1..2)=1), {f});
{f(w) = -3(-1) n+(-2) n}
> rsolve({y(n)=n*y(n-1), y(0)=1),y);
Г(n + 1)
> rsolve((y(n)*y(n-1)+y(n)-y(n-1)=0,у(0)=a},y);
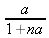
> rsolve({F(n)=F(n-1)+F(n-2),F(1..2)=1),F, 'genfunc'(x));
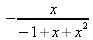
> rsolve({y(n+1)+f(n)=2*2^n+n, f(n+1)-y(n)=n-2^n+3, y(k=1..5)=2^k-1,f(5)=6), {y, f});
{f(n)=n+1, y(n) = 2 n- 1}
А теперь приведем результат вычисления функцией rsolve n-го числа Фибоначчи. Оно задается следующим выражением:
> eq1 := (f(n+2) = f(n+1) + f(n), f(0) = 1, f(1) = 1};
eq1 := {f(n+2) = f(n+1)+f(n), f(0) = 1, f(1) = 1}
В нем задана рекуррентная формула для числа Фибоначчи — каждое новое число равно сумме двух предыдущих чисел, причем нулевое и первое числа равны 1. С помощью функции rsolve в Maple 9.5 можно получить поистине ошеломляющий результат:
Читать дальше
Конец ознакомительного отрывка
Купить книгу