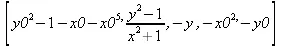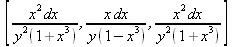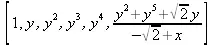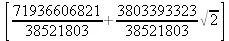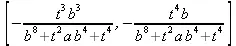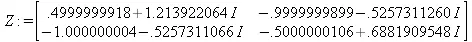periodmatrix(f, х, у, opt) — вычисляет периодическую матрицу кривой;
plot_knot(f,x,y,opt) — строит узел — несамопересекающуюся замкнутую кривую в трехмерном евклидовом пространстве;
puiseux(f,x=p,y,n,T) — определяет Пуизе-расширение алгебраической функции (может иметь и более простые формы записи);
singularities(f,x,y) — анализирует кривую на сингулярность.
4.10.2. Примеры работы с алгебраическими кривыми
Приведем также примеры применения функций пакета Algcurves (файл algcurve):
> Weierstrassform((y^2-1)^2+x*(x^2+1)^2, x,y,x0,y0);
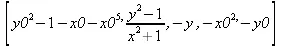
> f:=у^3+х^3*у^3+х^4;
f := y 3+ y 3x 3+ x 4
> differentials(f, х, у);
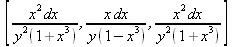
> differentials(f,x,у,skip_dx);
[x², yx, yx²]
> nops(%);
3
> genus(f, x, y);
3
> homogeneous(f, x, y, z);
x 4z 2+y 3x 3+у 3x 3
> g := y^3-х*y^2+2*2^(1/2)*y^2+х^2-2*2^(1/2)*х+2+y^6;
g := y 3- xy 2+ 2√2 у 2+ x 2- 2√2x + 2 + y 6
> integral_basis(g,x,y);
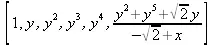
> is_hyperelliptic(f, x, y);
false
> f1:=у^2+х^5+1:is_hyperelliptic(f1, x, y);
true
> j_invariant(g,x,y);
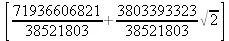
> parametrization(х^4+y^4+а*х^2*y^2+b*y^3,х,y,t);
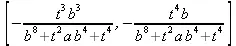
> Z := periodmatrix(f1,х,у,Riemann);
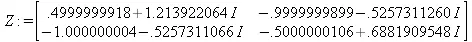
4.10.3. Построение алгебраических кривых класса knot
Функция plot_knot позволяет строить одну или несколько алгебраических кривых — узлов. Пример построения целого семейства узлов показан на рис. 4.37.

Рис. 4.37. Семейство узлов
Для лучшего обзора таких кривых рекомендуется воспользоваться возможностью вращения трехмерных фигур мышью для уточнения угла, под которым рассматривается фигура — в нашем случае семейство алгебраических кривых.
Начиная с версии Maple 7 в пакет расширения Algcurves добавлена новая функция импликативной графики plot_real_curve. Она строит алгебраическую кривую для действительной части полиномиального выражения и записывается в виде:
plot_real_curve(р, х, у, opt)
Функция имеет следующие параметры:
p — полиномиальное выражение переменных x и у задающее алгебраическую кривую;
opt — параметр, который может быть записан в форме приведенных ниже выражений:
showArrows=true или false — задает показ стрелок касательных или перпендикулярных к точкам вдоль кривой (по умолчанию false);
arrowIntervalStep=posint — задает число точек, пропускаемых до показа очередной пары стрелок (по умолчанию 10);
arrowScaleFactor=positive — задает масштаб для длины стрелок (по умолчанию 1);
colorOfTangentVector=с — задает цвет касательных стрелок, по умолчанию заданный как зелёный, COLOR(RGB,0,1.0);
colorOfNormalVector=с — задает цвет перпендикулярных стрелок, по умолчанию заданный как красный, COLOR(RGB,1,0,0);
colorOfCurve=с — задает цвет кривой, по умолчанию заданный как синий, COLOR(RGB, 0, 0, 1);
eventTolerance=positive — задает погрешность при представлении сингулярных точек (по умолчанию 0,01).
NewtonTolerance=positive — задает погрешность при выполнении ньютоновских итераций в ходе построений.
Функция plot_real_curve вычисляет и строит алгебраическую кривую по точкам. Применение функции plot_real_curve показывает рис. 4.38.

Рис. 4.38. Примеры применения функции plot_real_curve
4.11. Векторные вычисления и функции теории поля
4.11.1. Пакет векторных вычислений VectorCalculus
В Maple 8 были существенно расширены возможности вычислений над векторами (пространственными объектами) и поверхностями. Для этого введен пакет VectorCalculus, который, при вызове, открывает доступ ко многим командам и функция векторного анализа, теории поля и приложений дифференциального исчисления [67, 68] (файл vc):
> restart; with(VectorCalculus); interface(showassumed=0);
Warning, the assigned names <,> and <|> now have a global binding
Warning, these protected names have been redefined and unprotected:
*, +, Vector, diff, int, limit, series
[&x, *, +, ., <, >, <|>, AddCoordinates, ArcLength, BasisFormat, Binormal, CrossProduct, Curl, Curvature, Del, DirectionalDiff, Divergence, DotProduct, Flux, GetCoordinateParameters, GetCoordinates, Gradient, Hessian, Jacobian, Laplacian, LineInt, MapToBasis, Nabla, PathInt, PrincipalNormal, RadiusOfCurvature, ScalarPotential, SetCoordinateParameters, SetCoordinates, SurfaceInt, TNBFrame, Tangent, TangentLine, TangentPlane, TangentVector, Torsion, Vector, VectorField, VectorPotential, Wronskian, diff, evalVF, int, limit, series]
Нетрудно заметить, что данный пакет после загрузки видоизменяет многие операторы, команды и функции, встроенные в ядро системы. При этом меняется их математический и физический смысл. Поэтому пользоваться пакетом надо с известной осторожностью. Для восстановления роли функций можно использовать команду restart.
Читать дальше
Конец ознакомительного отрывка
Купить книгу