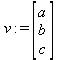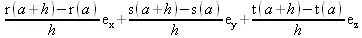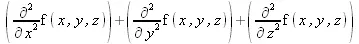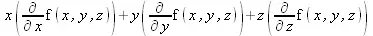Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Пакет VectorCalculus ориентирован в первую очередь на решение задач математической физики, использующих методы теории поля и приложения дифференциального исчисления. Он оперирует такими привычными для физиков (разумеется, и для математиков) понятиями, как поток векторного поля, градиент, тор-сион, векторный потенциал и др. Приведенный ниже материал поясняет применение большинства функций этого пакета. Полезно просмотреть и файл VectorCalculus.mws, содержащий примеры его применения. В Интернете можно найти целую серию уроков по векторному анализу и теории поля в виде пакета Calculus IV или V (разработчик проф. J. Wagner).

Вектор в геометрическом представлении в данном пакете по умолчанию задается в прямоугольной системе координат:

> v := Vector( [x,y,z]);

Здесь е х , е у и е z — проекции единичного вектора ена оси координат х, у и z. Тип координатной системы (по умолчанию — прямоугольная) можно определить следующим образом:

> attributes(v);

Для создания векторного поля служит функция

VectorField(v, с)

где v — вектор и с — опционально заданный параметр в форме name[name, name,...], задающий тип координатной системы.

Можно изменить систему координат, например, задав (с помощью функции установки координат SetCoordinates) полярную систему координат:

> SetCoordinates(polar);

> w := ;

> attributes(w);

Аналогично можно задать вектор в сферической системе координат:

> SetCoordinates(spherical[r,phi,theta]);

> F := VectorField();

> attributes(F);

Можно также сменить формат представления вектора и выполнить с ним некоторые простейшие векторные операции:

> BasisForrnat(false);

> v := ;

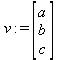
> BasisFormat(true);

> v;

> SetCoordinates(polar);

> MapToBasis(, 'cartesian');

> SetCoordinates(spherical);

> MapToBasis(, 'cartesian');

> SetCoordinates(spherical[r,phi,theta]);

> MapToBasis(VectorField(), 'cartesian'[x,y,z]);

Пакет VectorCalculus предусматривает возможность задания новой системы координат с помощью команды:

AddCoordinates(newsys, eqns, owrite)

где newsys — спецификация новой системы координат в виде symbol[name, name, …]; eqns — соотношения между координатами новой системы и прямоугольной системы координат, представленные в виде list(algebraic); owrite — заданное опционально равенство.

В данном пакете переопределены некоторые основные операции над векторами. Прежде всего, это операции сложения (+) и скалярного умножения (*), которые поясняются следующими примерами (файл vop) :

> SetCoordinates(cartesian);

> + m*;

> ( - ) / h;

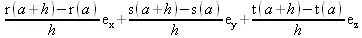
> limit(%,h=0);

Обратите внимание на вычисление предела в конце этих примеров. Далее можно отметить операцию точечного умножения, которая иллюстрируется следующими вполне очевидными примерами:

> . ;

> SetCoordinates(polar);

> . ;

> combine(%,trig);

> SetCoordinates(cartesian[x,y,z]);

> Del . VectorField(<���х^2,у^2,z^2>);

> Del . Del;

> (Del . Del) (f(x,y,z));

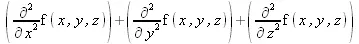
> L := VectorField( ) . Del;

> L(f(x,y,z));

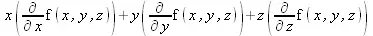
Определена также операция кросс-умножения:

> &х ;

> SetCoordinates(cylindrical);

> &x ;

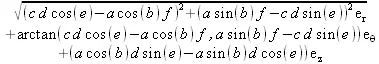
> SetCoordinates(cartesian[x,y,2]);