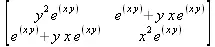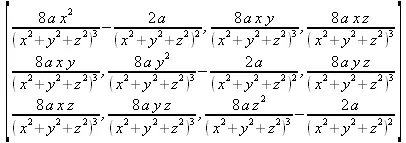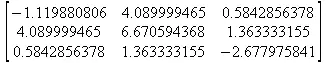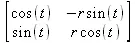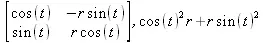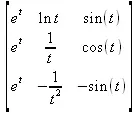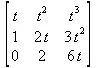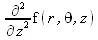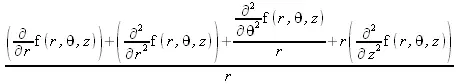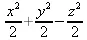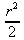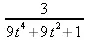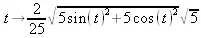Примеры задания таких матриц приведены ниже (файл vecmatrix):
> Hessian(ехр(х*y), [х,y]);
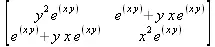
> Hessian(а/(х^2+y^2+z^2), [х, y, z]);
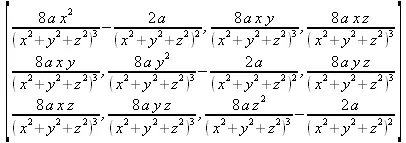
> Н := unapply(%, [a,x,y,z]):
> Н(1/2, 0.3, 0.7, 0.1);
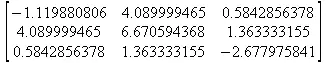
> Jacobian([r*cos(t), r*sin(t)], [r,t]);
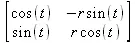
> Jacobian([r*cos(t), r*sin(t)], [r,t], 'determinant');
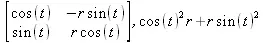
> Wronskian([exp(t),ln(t),sin(t)], t);
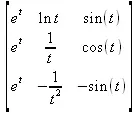
> Wronskian([t, t^2, t^3], t)
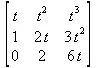
4.11.7. Функции теории поля
К основным функциям теории поля относятся:
Curl(F) — вычисляет вихрь векторного поля в R³;
Divergence(F) — вычисляет дивергенцию векторного поля;
Flux(f, dom) — вычисляет поток векторного поля в R³;
Gradient(f, с) — вычисляет градиент функции f в пространстве от R nдо R;
Del(f, с) и Nabla(f, с) — векторные дифференциальные операторы;
Laplacian(f, с) или Laplacian(F) — вычисляет лапласиан функции f или векторного определения (процедуры) F;
ScalarPotential(v) — вычисляет скалярный потенциал векторного поля;
Torsion(C, t) — вычисляет торсион в R³;
VectorPotential(v) — вычисляет векторный потенциал в R³;
Довольно громоздкие определения этих функций, основанные на использовании криволинейных и поверхностных интегралов, имеются в учебной литературе. Не приводя их, ограничимся приведенными ниже примерами применение указанных выше функций (файл vecft):
> restart:with(VectorCalculus): SetCoordinates('cartesian'[x,y,z]);
cartesian x, у, z
> F := VectorField( <-y,x,0> );
F:=-yē x+хē у
> Curl(F);
2ē z
> Del &x F;
2ē z
> Nabla &x F;
2ē
> CrossProduct(Del, F);
2ē z
> F := VectorField(<���х^2,y^2,z^2>);
F:=-x²ē х+ y²ē у+ z²ē z
> Divergence(F);
2х + 2у + 2z
> Flux(VectorField(, cartesian[x,y,z]), Sphere(<0,0,0>, r));
4r³ π
> Gradient(х^3/3+у^2, [x,y]);
x²ē x+ 2yē у
0ē х
> Del(х^2+у^2+z^2);
2xē x+ 2уē у+ 2zē z
> Nabla(х^2+у^2+z^2);
2xē x+ 2уē у+ 2zē z
> Del . %;
6
> Laplacian(х^2+у^2+z^2, [x,y,z]);
6
> Laplacian(f(r,theta,z));
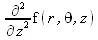
> SetCoordinates('cylindrical' [r, theta, z])
cylindrical r, θ, z
> Laplacian(f(r, theta, z));
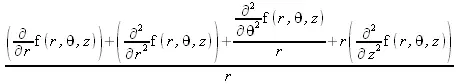
> SetCoordinates('cartesian'[x,y,z]);
cartesian x, y, z
> v := VectorField();
v := xē x+ уē у- zē z
> ScalarPotential(v);
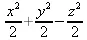
> v := VectorField(<-y,0,z>);
v := -yē x+ zē z
> ScalarPotential(v); den := х^2 + y^2 + z^2;
den := x² + y² + z²
> ScalarPotential((x,y,z) -> /den);
(x,y,z)→½ ln(x² + y² + z²)
> SetCoordinates('spherical'[r,phi,theta]);
spherical r, φ, θ
> v := VectorField();
v:= r ē г
> ScalarPotential(v);
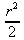
> restart:with(VectorCalculus): simplify( Torsion()) assuming t::real;
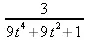
> Torsion(t -> <2*t,sin(t),cos(t)>);
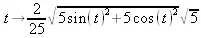
> SetCoordinates('cartesian'[x,y,z]); v := VectorField();
cartesian x, y, z
v:= уē x- хē у
> VectorPotential(v);
-xzē x- yzē у
> SetCoordinates('cylindrical'[r,theta,z]);
cylindrical r, θ, z
> v := VectorField();
v:= rē r-2zē z
> VectorPotential(v);
(-r sin(θ)² z - r cos(θ)² z) ē θ
> simplify(Curl(%));
rē r- 2zē z
Обратите внимание на то, что для гарантии правильного выполнения этих команд и отсутствия «зависания» компьютера может потребоваться команда restart и перезагрузка пакета VectorCalculus.
4.11.8. Приближение площади сложной поверхности суммами Римана
Одним из важнейших приложений пакета VectorCalculus является вычисление длин дуг и площадей сложных поверхностей на основе применения линейных и поверхностных интегралов. Иногда это встречает большие трудности и требует специальных подходов. Примером может служить поверхность, заданная рис. 4.40. Эта поверхность построена с имитацией ее освещения от внешнего источника света.
Читать дальше
Конец ознакомительного отрывка
Купить книгу