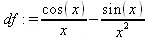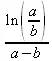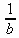Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Функциональная зависимость или функция f(х) даже от одной переменной может быть достаточно сложной, содержать корни (значения x при которых f(х)=0), полюса (значения х при которых f(х)→∞), максимумы и минимумы, разрывы, асимптотические значения, точки перегиба и т.д. Часто эти особенности видны на графике зависимости f(х), но анализ функциональной зависимости предполагает, что эти особенности могут быть точно идентифицированы и определены по математическому выражению, представляющему зависимость. Например, поиск корней сводится к решению уравнения f(х)=0 в заданном интервале, поиск экстремумов полагает нахождение значений x в точках экстремумов и значений f(х) в них и т.д.

К сожалению, пока нет средств, сразу выявляющих все особенности функциональных зависимостей, поскольку даже средства, решающие частные задачи анализа функций, довольно сложны и специфичны. Достаточно отметить проблему поиска экстремумов функций (особенно функций нескольких переменных). Поэтому функции приходится анализировать индивидуально.

С помощью функции fsolve системы Maple легко находятся значения независимой переменной x функций вида f(x), при которых f(х)=0 ( корни этого уравнения). При этом данная функция позволяет (в отличие от функции solve) изолировать корни функции f(х) указанием примерного интервала их существования.

Для простых функций одной переменной f(х) поиск экстремумом часто сводят к нахождению точек, в которых первая производная f(х) обращается в нуль. Для этого можно использовать также функцию fsolve (иногда и solve, но она дает вывод в более сложной форме). Приведем пару примеров (файл extrem):

> у:=expand((х-3)*(х-1)*х*(х+2));

> dy:=simplify(diff(y,х));

> plot({y,dy},х=-3..3,-10..10,color=black,thickness=[2,1]);

> extrem:=fsolve(dy=0,х);

В этом примере создан полином y с корнями 3, 1, 0 и -2 и найдена его производная dy. На рис. 5.1 построены графики функции и ее производной (жирная кривая). Из него видно, что полином p имеет экстремумы в точках, лежащих в промежутках между корневыми точками. Их значения и найдены как значения переменной extrem, для которых вторая производная равна 0. Рекомендуется проверить вид вывода, если fsolve заметить на solve.

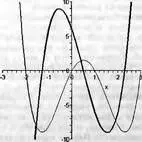
Рис. 5.1. График функциональной зависимости — полинома и ее производной

Возьмем еще один пример для поиска экстремумов выражения sin(x)/x. Это выражение имеет бесконечное число экстремумов слева и справа от х=0 (в этой точке расположен главный максимум со значением 1). Ограничимся поиском трех экстремумов в интервале изменения x от 3 до 12:

> f:=sin(х)/x:df:=diff(f,x);

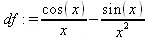
> plot({ f, df},x=0..12,color=black,thickness=[2,1]):

> [fsolve(df,x=3..6),fsolve(df,x=7..9),fsolve(df,x=9..12)];

Тут уже приходится искать каждый экстремум поодиночке, задавая поиск в соответствующем интервале изменения х. Для просмотра графика функциональной зависимости и ее производной достаточно в конце второй строки ввода заменить знак «:» на «;».

Функция solve нередко позволяет найти экстремумы в аналитическом виде как нули первой производной. Приведем примеры этого (файл extrem):

> restart:y:=ехр(-а*х)-exp(-b*x);dy:=diff(y,х);

> solve(dy,x);

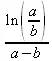
> restart:y:=а*х*ехр(-b*x);dy:=diff(y,х);

> solve(dy,x);

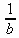
Этот метод иногда можно распространить на случай ряда переменных. Ниже представлен такой пример для функции двух переменных:

> restart:

> z:=(х,y)-> а*х^2 + b*х*y + с*y^2 + d*(х-y);

> xy:=solve({diff(z(x,y),x) = 0, diff(z(x,y),y) = 0},{х,y});