Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Часто необходимо найти минимум некоторой функции при наличии ограничений на значения независимых переменных. Ниже рассматривается нетривиальная задача такого рода, решаемая методом выпуклого программирования (разновидность нелинейного программирования) — файл minp.

Пусть надо найти минимум функции f:=х1^2+(х2–1)^2 при следующих ограничениях: 2x1+х2>=7, x1+2*х2>=5, x1>=0 и х2>=0. Составим на основе этого функцию Лагранжа:

> F:=x1^2+(х2-1)^2+y1*(7-2*х1-х2)+y2*(5-х1-2*х2);

и найдем ее частные производные:

> F1:=diff(F,x1);

> F2:=diff(F,x2);

> F3:=dxff(F,y1);

> F4:=diff(F,y2);

Соберем воедино все равенства и неравенства этой задачи:

> eq:={Fl=u1,F2=u2,x1*F1,x2*F2,F3+v1,F4+v2,y1*F3,y2*F4,

x1>=0,x2>=0,y1>=0,y2>=0,u1>=0,u2>=0,v1>=0,v2>=0};

Первые шесть равенств соответствуют теореме Куна-Такера о том, что в точке минимума существуют целые неотрицательные числа u1, u2 , v1 и v2 для которых выполняются эти шесть равенств (обратите внимание на то, что запись только левой части равенства означает, что она приравнивается к 0). Теперь с помощью функции solve можно найти решение данной задачи:

> solve(eq,{x1,х2,y1,y2,u1,u2,v1,v2});

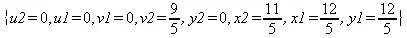
Таким образом, на указанном множестве функция достигает минимума в точке (12/5, 11/5).

Для исследования функций на непрерывность (отсутствие разрывов) Maple имеет функцию iscont, записываемую в ряде форм:

iscont(expr, х = а..b)

iscont(expr, х = а..b, 'closed')

iscont(expr, х = а..b, 'open')

Она позволяет исследовать выражение expr, заданное в виде зависимости от переменной х, на непрерывность. Если выражение непрерывно, возвращается логическое значение true, иначе — false. Возможен также результат типа FAIL. Параметр 'closed' показывает, что конечные точки должны также проверяться, а указанный по умолчанию параметр 'open' — что они не должны проверяться.

Работу функции iscont иллюстрируют следующие примеры (файл fanal):

> iscont(1/х^2,х=-1..1);

> iscont(1/х^2,х=-1..1,'closed');

> iscont(1/x,х=0..1);

> iscont(1/x,x=0..1,'closed');

> iscont(1/(x+a),x=-1..1);

Рекомендуется внимательно присмотреться к результатам этих примеров и опробовать свои собственные примеры.

Функции, не имеющие непрерывности, доставляют много хлопот при их анализе. Поэтому важным представляется анализ функций на непрерывность. Начиная с Maple 7, функция discont(f,x) позволяет определить точки, в которых нарушается непрерывность функции f(x). Она вычисляет все точки в пределах изменения х от –∞ до +∞. Результаты вычислений могут содержать особые экстрапеременные с именами вида _Zn~ и _NNn~. В частности, они позволяют оценить периодические нарушения непрерывности функций. Примеры применения функции discont приведены ниже (файл fanal):

> discont(1/(х-2),х);

> discont(1/((х-1)*(х-2)*(х-3)),х);

> discont(GAMMA(х/2),х);

Весьма рекомендуется наряду с применением данной функции просмотреть график анализируемой функции.

Еще раз полезно обратить внимание на то, что в ряде примеров в выводе используются специальные переменные вида _NameN~ , где Name — имя переменной и N — ее текущий номер. После выполнения команды restart отсчет N начинается с 1. Если вывод с такими переменными уже применялся, то их текущие номера могут казаться произвольными. Специальные переменные часто используются для упрощения выводимых выражений.