Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

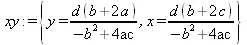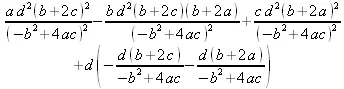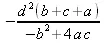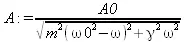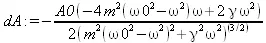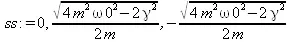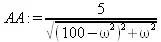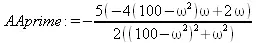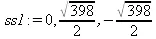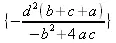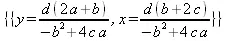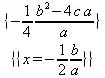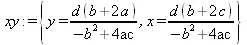
> z(rhs(xy[2]),rhs(xy[1]));

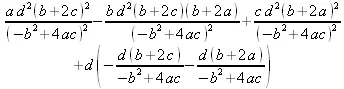
> simplify(%);

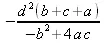
Разумеется, подобное решение возможно далеко не всегда, хотя и частные решения данной задачи представляют значительный практический интерес.

Одной из практически важных задач может служить нахождение пика амплитудно-частотной характеристики слабо демпфированной системы с массой m и частотой собственных колебаний ω0. Эту характеристику можно представить следующим известным выражением (файл afc):

> restart;

> A:=A0/sqrt(m^2* (omega0^2-omega^2)^2+gamma^2*omega^2);

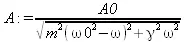
Найдя ее производную и, вычислив корни последней, получим:

> dA:=diff(A,omega);

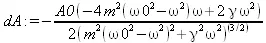
> ss:=solve(dA=0,omega);

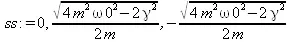
Из этих трех частот только одна физически реальна — средняя. Остальные могут быть отброшены. А теперь приведем пример с конкретными числовыми данными:

> AA:=subs(А0=5,omega0=10,m=1, gamma=1, А);

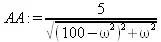
> AAprime :=diff(АА, omega);

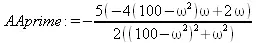
> ss1:=solve(AAprime=0,omega);

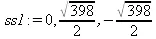
> evalf(ss1);

Нетрудно подметить, что частота пика амплитудно-частотной характеристики чуть меньше частоты собственных колебаний системы.

Ряд функций служит специально для вычисления экстремумов , максимумов и минимумов функций, а также для определения их непрерывности. Одна из таких функций extrema позволяет найти экстремумы выражения expr (как максимумы, так и минимумы) при ограничениях constrs и переменных vars, по которым ищется экстремум:

extrema(expr, constrs)

extrema(expr, constrs, vars)

extrema(expr, constrs, vars, 's')

Ограничения contrs и переменные vars могут задаваться одиночными объектами или списками ряда ограничений и переменных. Найденные координаты точки экстремума присваиваются переменной 's'. При отсутствии ограничений в виде равенств или неравенств вместо них записывается пустой список {}.

Эта функция в предшествующих версиях Maple находилась в стандартной библиотеке и вызывалась командой readlib(extrema). Но начиная с Maple 7 ее можно использовать без предварительного объявления. В этом убеждают приведенные ниже примеры (файл extrema):

> restart:

> z:=(х,y)-> а*х^2 + b*x*y + с*y^2 + d*(х-y);

> extrema(z(х,y),{},{х,y},'s');

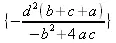
> s;

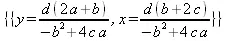
> extrema(а*х^2+b*х+с,{},x,'s');s;

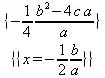
> extrema(х*ехр(-х),{}, х, 's'); s;

> extrema(sin(x)^2,{},x,'s');s;

> extrema(х+у/z,х^2+у^2+z^2=1,{x,y,z},'s');s;

> evalf(%);

Как видно из приведенных примеров, функция extrema возвращает как значения экстремумов, так и значения аргументов, при которых экстремумы наблюдаются. Обратите внимание, что в первом примере результат вычисления экстремума функции z(x,y) оказался тем же, что и в предшествующем разделе. Это говорит в пользу применения функции extrema.