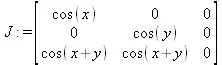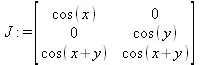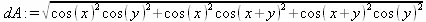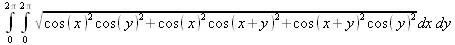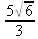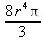
Рис. 4.40 Сложная поверхность с эффектами ее освещения внешним источником света
Применим обычную процедуру вычисления площади поверхности. Для этого вычислим для нее матрицу якобиана и удалим из нее столбец с нулевыми элементами (файл vecrim):
> J := Jacobian(f, [х, у, z]);
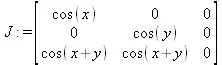
> J := DeleteColumn(J, [3]);
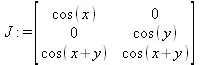
Тогда площадь поверхности вычисляется следующим образом:
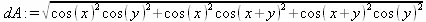
> Int(Int(dA, x=0..2*Pi), y=0..2*Pi);
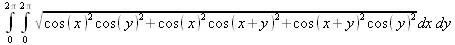
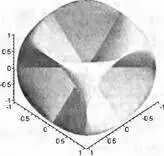
К сожалению, этот двойной интеграл Maple не вычисляет из-за сложности подынтегрального выражения, график которого представлен на рис. 4.41.
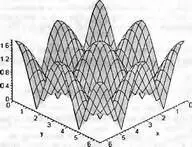
Рис. 4.41. График подынтегрального выражения
Для приближенного вычисления площади можно разбить поверхность на достаточное число сегментов и использовать замену интегралов суммами Римана. Оценка нижней и верхней сумм Римана для четверти поверхности (ее одного квадранта) представлена ниже:
> for s from 1 to 8 do
F := (k, t)->subs({x=k*Pi/(10*s), y=t*Pi/(10*s)}, dA):
A||s := evalf((Pi/<10*s))^2*sum(sum(F(p, q), p=0..10*s-1), q=0..10*s-1)):
print(A||s);
end do:
7.408455387
7.429353779
7.429810700
7.429973244
7.430045037
7.430081583
7.430102033
> for s from 1 to 8 do
F := (k, t)->subs({x=k*Pi/(10*s), y=t*Pi/(10*s)}, dA):
Alls := evalf((Pi/(10*s))^2*sum(sum(F(p, q), p=1..10*s),
q=1..10*s)):
print(A||s)
end do:
7.408455386
7.427471278
7.429353778
7.429810700
7.429973260
7.430045062
7.430081587
7.430102036
Поскольку эти суммы явно сходятся, то можно считать применение сумм Римана приемлемым и принять, что площадь данной поверхности приближенно равна:
> Area := 4*7.43;
Area:= 29.72
4.11.9. Вычисление поверхностных интегралов
Приведенный выше пример иллюстрирует трудности вычислений поверхностных интегралов. Разумеется, далеко не всегда Maple требует специальных подходов к вычислению подобных интегралов и многие из них благополучно вычисляются.
Для этого используется функция:
SurfaceInt(f, dom, inert)
где f — алгебраическое выражение, задающее интегрируемую зависимость, dom — спецификация поверхности в виде list(name)=surface и inert — имя, задаваемое как опция.
Примеры применения данной функции представлены ниже (файл surint):
> with(VectorCalculus):
> SurfaceInt(1, [x,y,z] = Surface(, s=0..Pi/2, t=0..Pi, coords=spherical)) assuming r>0;
π r²
>SurfaceInt(x+y+z, [x,y,z] = Surface(, [s,t] = Triangle(<0.0>,<1,0>,<1,1>)));
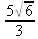
> SurfaceInt(2*y^2, [x,y,z] = Sphere(<0,0,0>, r));
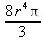
Глава 5
Анализ функциональных зависимостей и обработка данных
Аналитические функции и степенные многочлены (полиномы) широко используются в математике и физике. В этой главе описана работа с функциями и полиномами, включающая в себя традиционный анализ функций, выявляющий их особенности и обеспечивающий различные преобразования функций, вычисление и преобразование полиномов в том числе ортогональных и техника приближения (аппроксимации) функций и табличных данных полиномами и сплайнами. Все эти вопросы имеют исключительно важное значение в практике научно-технических расчетов.
5.1. Анализ функциональных зависимостей
5.1.1. Понятие о функциональных зависимостях
Говорят, что y(x) есть функция, если известно правило, согласно которому каждому значению аргумента x соответствует некоторое значение у. Мы уже сталкивались с элементарными и специальными математическими функциями, которые имеют свои уникальные имена. Возможны и функции двух и более переменных, например функции Бесселя разного порядка.
Здесь мы под функциональной зависимостью будем понимать не только зависимости, заданные отдельными элементарными или специальными функциями, но и любые зависимости какой либо величины от ряда других величин — переменных. Такие выражения могут содержать ряд элементарных или специальных математических функций. Например, sin(x) и cos(x) это просто элементарные функции, а f(х)=2*sin(x)*cos(x) это уже функциональная зависимость f от х. Любое математическое выражение, содержащее переменные х, y, z, … можно рассматривать как функциональную зависимость f(x, y, z, …) от этих переменных.
Читать дальше
Конец ознакомительного отрывка
Купить книгу