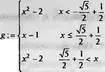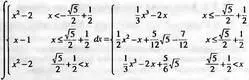Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

С функциями типа piecewise можно работать как с обычными функциями. При этом необходимые операции и преобразования осуществляются для каждой из частей функции и возвращаются в наглядной форме.

Ниже приведен пример задания функции f в аналитической форме (файл piecewi):

> restart;

> f := max(х^2 - 2, x-1);

Для выявления характера функции воспользуемся функцией convert и создадим объект g в виде кусочной функции:

> g := convert(f, piecewise);

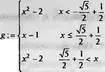
Выполним дифференцирование и интегрирование функции:

> fprime := diff(f, х);

> Int(g,х)=int(g,х);

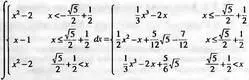
Как нетрудно заметить, результаты получены также в виде кусочных функций. Можно продолжить работу с функцией f и выполнить ее разложение в степенной ряд:

> series(f, х);

Чтобы убрать член с остаточной погрешностью, можно выполнить эту операцию следующим образом:

> series(g, х);

Обратите внимание на то, что поскольку разложение в ряд ищется (по умолчанию) в окрестности точки х= 0, то при этом используется только тот кусок функции, в котором расположена эта точка.

К числу наиболее известных и изученных аналитических функций относятся степенные многочлены — полиномы. Графики полиномов описывают огромное разнообразие кривых на плоскости. Кроме того, возможны рациональные полиномиальные выражения в виде отношения полиномов. Таким образом, круг объектов, которые могут быть представлены полиномами, достаточно обширен, и полиномиальные преобразования широко используются на практике, в частности, для приближенного представления других функций.

Под полиномом в СКМ сумма выражений с целыми степенями. Многочлен для ряда переменных — многомерный полином. К одномерным полиномам относятся степенной многочлен

а также отдельная переменная х и константа. Большое достоинство полиномов состоит в том, что они дают единообразное представление многих зависимостей и для своего вычисления требуют только арифметических операций (их число значительно сокращается при использовании хорошо известной схемы Горнера). Производные от полиномов и интегралы с подынтегральными функциями-полиномами легко вычисляются и имеют простой вид. Есть и достаточно простые алгоритмы для вычисления всех (в том числе комплексных) корней полиномов на заданном промежутке.

Для выделения коэффициентов полиномов в Maple служат следующие функции:

coeff(p, х) — возвращает коэффициент при х полинома p;

coeff(p, x, n) — возвращает коэффициент для члена со степенью n полинома p;

coeff(p, x^n) — возвращает коэффициенты при x^n полинома p;

coeffs(p, х, 't') — возвращает коэффициенты полинома нескольких переменных, относящиеся к переменной x (или списку переменных) с опцией 't', задающей имя переменной;

collect(p, x) — возвращает полином, объединяя коэффициенты при степенях переменной х.

Ниже даны примеры применения этих функций (файл coefcoll):

> р:=а4*х^4+а3*х^3+а2*х^2+а1*х+а0;

> coeff(р,х);

> coeff(р,х^3);

> coeff(р,х,4);

> coeffs(p,x);

> q:=x^2+2*y^2+3*x+4*y+5;

> coeffs(q);

> coeffs(q,y);

> coeffs(q,x,y);

> collect(q,x);

> collect(q,x,y);

Дополнительные примеры на применение функции collect можно найти в файле collect.