Pedro Domingos - The Master Algorithm - How the Quest for the Ultimate Learning Machine Will Remake Our World

On a lighter note, Microsoft’s Xbox Live uses a Bayesian network to rate players and match players of similar skill. The outcome of a game is a probabilistic function of the opponents’ skill levels, and using Bayes’ theorem we can infer a player’s skill from the outcomes of his games.

The inference problem

There’s a big snag in all of this, unfortunately. Just because a Bayesian network lets us compactly represent a probability distribution doesn’t mean we can also reason efficiently with it. Suppose you want to compute P(Burglary | Bob called, Claire didn’t) . By Bayes’ theorem, you know this is just P(Burglary) P(Bob called, Claire didn’t | Burglary) / P(Bob called, Claire didn’t) , or equivalently, P(Burglary, Bob called, Claire didn’t) / P(Bob called, Claire didn’t) . If you had the full table with the probabilities of all states, you could obtain both of these probabilities by adding up the corresponding lines in the table. For example, P(Bob called, Claire didn’t) is the sum of the probabilities of all the lines where Bob calls and Claire doesn’t. But the Bayesian network doesn’t give you the full table. You could always construct it from the individual tables, but that takes exponential time and space. What we really want is to compute P(Burglary | Bob called, Claire didn’t) without building the full table. That, in a nutshell, is the problem of inference in Bayesian networks.

In many cases we can do this and avoid the exponential blowup. Suppose you’re leading a platoon in single file through enemy territory in the dead of night, and you want to make sure that all your soldiers are still with you. You could stop and count them yourself, but that wastes too much time. A cleverer solution is to just ask the first soldier behind you: “How many soldiers are behind you?” Each soldier asks the next the same question, until the last one says “None.” The next-to-last soldier can now say “One,” and so on all the way back to the first soldier, with each soldier adding one to the number of soldiers behind him. Now you know how many soldiers are still with you, and you didn’t even have to stop.

Siri uses the same idea to compute the probability that you just said, “Call the police” from the sounds it picked up from the microphone. Think of “Call the police” as a platoon of words marching across the page in single file. Police wants to know its probability, but for that it needs to know the probability of the ; and the in turn needs to know the probability of call . So call computes its probability and passes it on to the , which does the same and passes the result to police . Now police knows its probability, duly influenced by every word in the sentence, but we never had to construct the full table of eight possibilities (the first word is call or isn’t, the second is the or isn’t, and the third is police or isn’t). In reality, Siri considers all words that could appear in each position, not just whether the first word is call or not and so on, but the algorithm is the same. Perhaps Siri thinks, based on the sounds, that the first word was either call or tell , the second was the or her , and the third was police or please . Individually, perhaps the most likely words are call , the , and please . But that forms the nonsensical sentence “Call the please,” so taking the other words into account, Siri concludes that the sentence is really “Call the police.” It makes the call, and with luck the police get to your house in time to catch the burglar.

The same idea still works if the graph is a tree instead of a chain. If instead of a platoon you’re in command of a whole army, you can ask each of your company commanders how many soldiers are behind him and add up their answers. Each company commander in turn asks each of his platoon commanders, and so on. But if the graph forms loops, you’re in trouble. If there’s a liaison officer who’s a member of two platoons, he gets counted twice; in fact, everyone behind him gets counted twice. This is what happens in the “aliens have landed” scenario, if you want to compute, say, the probability of panic:

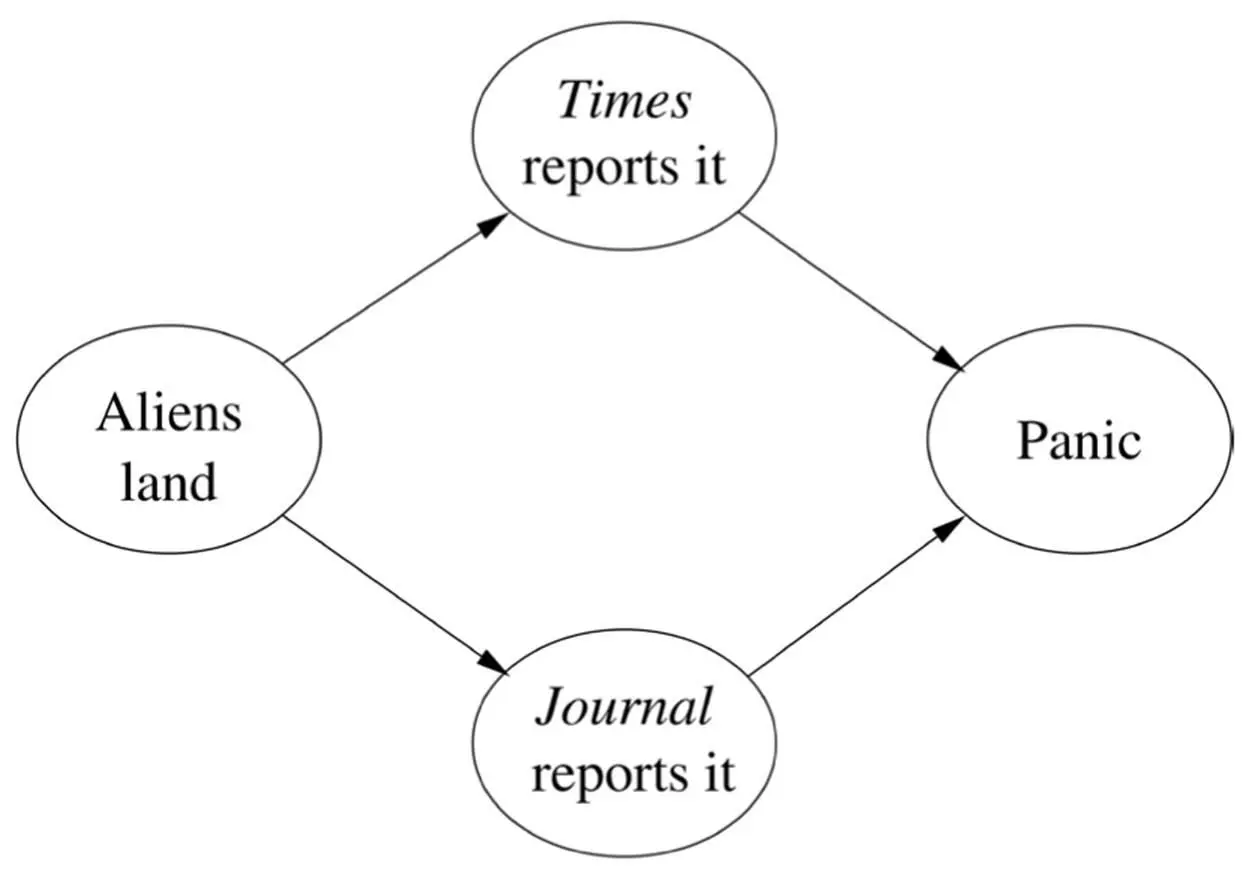
One solution is to combine The Times reports it and The Journal reports it into a single megavariable with four values: YesYes if they both do, YesNo if the Times reports a landing and the Journal doesn’t, and so on. This turns the graph into a chain of three variables, and all is well. However, every time you add a news source, the number of values of the megavariable doubles. If instead of two news sources you have fifty, the megavariable has 2 50values. So this method can only get you so far, and no other known method does any better.

The problem is worse than it seems, because Bayesian networks in effect have “invisible” arrows to go along with the visible ones. Burglary and Earthquake are a priori independent, but the alarm going off entangles them: the alarm makes you suspect a burglary, but if now you hear on the radio that there’s been an earthquake, you assume that’s what caused the alarm. The earthquake has explained away the alarm, making a burglary less likely, and the two are therefore dependent. In a Bayesian network, all parents of the same variable are interdependent in this way, and this in turn introduces further dependencies, making the resulting graph often much denser than the original one.

The crucial question for inference is whether you can make the filled-in graph “look like a tree” without the trunk getting too thick. If the megavariable in the trunk has too many possible values, the tree grows out of control until it covers the whole planet, like the baobabs in The Little Prince . In the tree of life, each species is a branch, but inside each branch is a graph, with each creature having two parents, four grandparents, some number of offspring, and so on. The “thickness” of a branch is the size of the species’ population. When the branches are too thick, our only choice is to resort to approximate inference.

One solution, left as an exercise by Pearl in his book on Bayesian networks, is to pretend the graph has no loops and just keep propagating probabilities back and forth until they converge. This is known as loopy belief propagation, both because it works on graphs with loops and because it’s a crazy idea. Surprisingly, it turns out to work quite well in many cases. For instance, it’s a state-of-the art method for wireless communication, with the random variables being the bits in the message, encoded in a clever way. But loopy belief propagation can also converge to the wrong answers or oscillate forever. Another solution, which originated in physics but was imported into machine learning and greatly extended by Michael Jordan and others, is to approximate an intractable distribution with a tractable one and optimize the latter’s parameters to make it as close as possible to the former.

The most popular option, however, is to drown our sorrows in alcohol, get punch drunk, and stumble around all night. The technical term for this is Markov chain Monte Carlo , or MCMC for short. The “Monte Carlo” part is because the method involves chance, like a visit to the eponymous casino, and the “Markov chain” part is because it involves taking a sequence of steps, each of which depends only on the previous one. The idea in MCMC is to do a random walk, like the proverbial drunkard, jumping from state to state of the network in such a way that, in the long run, the number of times each state is visited is proportional to its probability. We can then estimate the probability of a burglary, say, as the fraction of times we visited a state where there was a burglary. A “well-behaved” Markov chain converges to a stable distribution, so after a while it always gives approximately the same answers. For example, when you shuffle a deck of cards, after a while all card orders are equally likely, no matter the initial order; so you know that if there are n possible orders, the probability of each one is 1/ n . The trick in MCMC is to design a Markov chain that converges to the distribution of our Bayesian network. One easy option is to repeatedly cycle through the variables, sampling each one according to its conditional probability given the state of its neighbors. People often talk about MCMC as a kind of simulation, but it’s not: the Markov chain does not simulate any real process; rather, we concocted it to efficiently generate samples from a Bayesian network, which is itself not a sequential model.