Владимир Брюков - Как предсказать курс доллара. Эффективные методы прогнозирования с использованием Excel и EViews

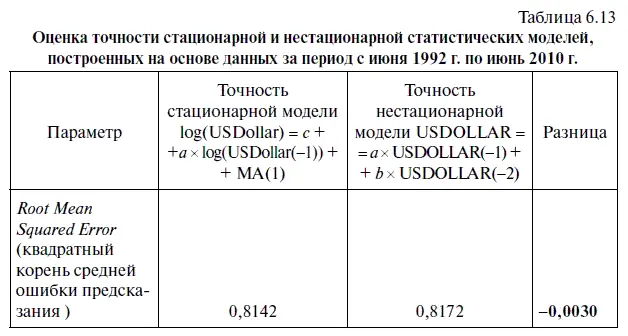
В результате мы получили табл. 6.13, в которой наряду с оценкой точности стационарной прогностической модели log(USDollar) = с + а × log(USDollar(-1)) + МА(1) поместили и оценку точности нестационарной статистической модели USDOLLAR = а × USDOLLAR(-l) + а × USDOLLAR(-2) за период с июня 1992 г. по июнь 2010 г.

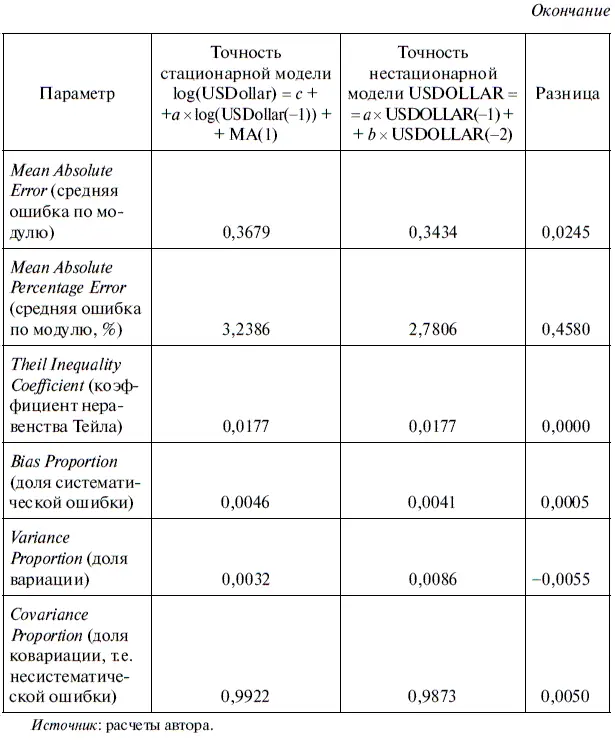
О содержательной интерпретации параметров, представленных в табл. 6.13, мы уже говорили (см. алгоритм действий № 8 «Как оценить точность статистической модели в EViews»).

Нетрудно заметить, что хотя в целом по уровню точности обе модели имеют довольно близкие оценки, тем не менее стационарная модель по ряду показателей уступает нестационарной модели. Так, довольно существенным кажется отклонение по величине средней ошибки по модулю (Mean Absolute Error) и по величине средней ошибки по модулю в процентах (Mean Absolute Percentage Error). Например, в целом за весь период средняя ошибка по модулю для стационарной модели оказалась на 2,45 процентного пункта выше, чем у нестационарной, а по величине средней ошибки по модулю в процентах — почти на 0,46 пункта.

Однако если посмотреть, как изменялась точность обеих статистических моделей в различные периоды времени, то начиная с 1999 г. стационарная модель дает более точные прогнозы. В частности, в период с января 1999 г. по июнь 2010 г. средняя точность стационарной модели оказалась выше точности нестационарной модели на 0,2 коп. по модулю (см. цифры, выделенные жирным шрифтом в табл. 6.14). А с января 2009 г. по июнь 2010 г. эта разница составила уже 8,7 коп.

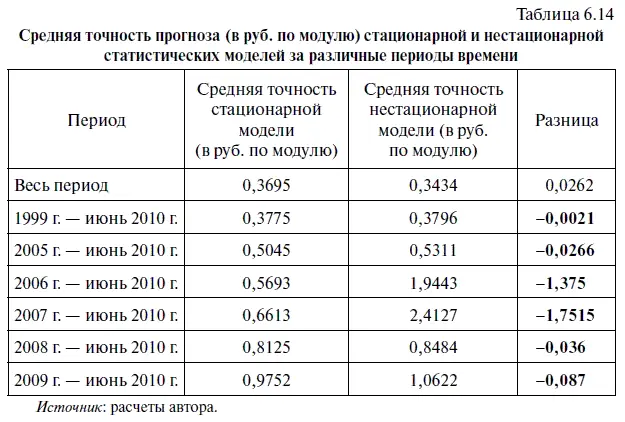
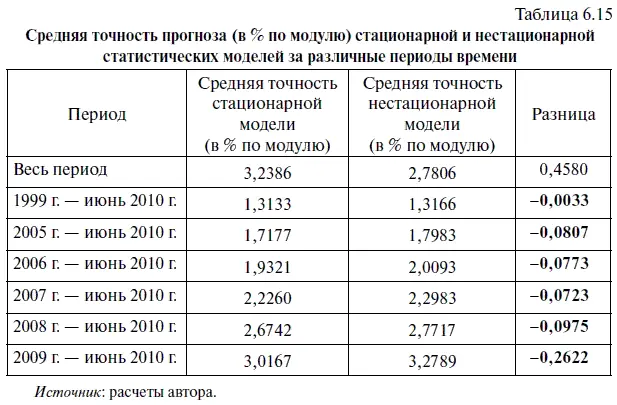
Естественно, что и по величине средней точности прогноза (в % по модулю) стационарная модель с января 1999 г. также дает более точные прогнозы. В частности, в период с января 1999 г. по июнь 2010 г. средняя точность стационарной модели (в % по модулю) оказалась выше точности нестационарной модели на 0,08 процентного пункта (см. цифры, выделенные жирным шрифтом в табл. 6.15). В свою очередь с января 2009 г. по июнь 2010 г. эта разница составила уже более 0,26 процентного пункта. С учетом этого можно сделать вывод, что точность стационарной статистической модели за последние 11,5 лет оказалась выше, чем у нестационарной модели.

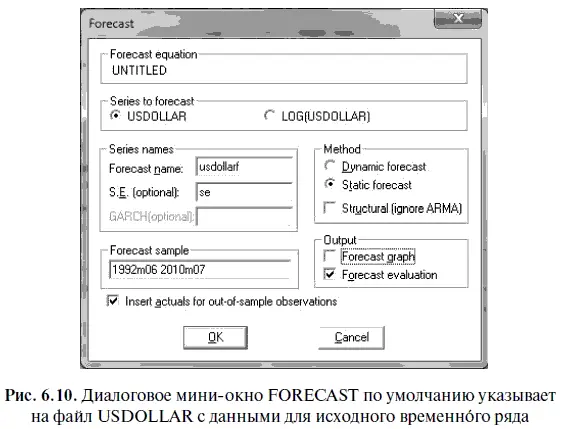
Воспользовавшись диалоговым мини-окном FORECAST, мы получили не только оценку точности прогноза для стационарной статистической модели log(USDollar) = с + а × log(USDollar(-1)) + МА(1), но и файл с точечными прогнозами USDOLLARF за период с июля 1992 г. по июль 2010 г. Открыв этот файл, мы выяснили, что точечный прогноз на июль 2010 г. оказался равен 31 руб. 19 коп., однако фактический курс доллара в июле 2010 г. был равен 30 руб. 19 коп. Следовательно, разница составила 1 руб. Посмотрим, попал ли фактический курс доллара в диапазон интервального прогноза?

Однако, прежде чем это сделать, проверим остатки, полученные по модели log(USDollar) = с + а × log(USDollar(-l)) + МА(1), на нормальное распределение и на стационарность (см. алгоритм действий № 9).

В первом случае откроем файл RESID и выберем опции VIEW (смотреть)/DESCRIPTIVE STATISTICS (описательная статистика)/ STATS TABLE (таблица со статистикой). При этом следует иметь в виду, что проверку на нормальное распределение остатков целесообразно проводить относительно логарифмических остатков, поскольку наша статистическая модель построена на логарифмическом временном ряде. Логарифмические остатки нетрудно найти, если при составлении прогнозов в диалоговом мини-окне FORECAST (прогноз) поставим «галочку» у файла LOG(USDOLLAR) (см. рис. 6.6). В результате мы получили табл. 6.16.

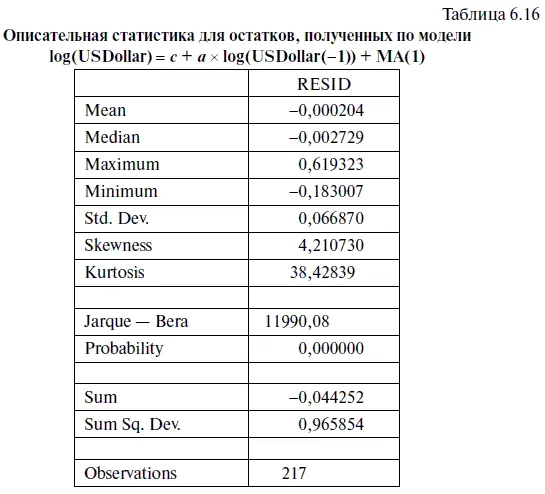
Судя по тому, что коэффициент асимметрии ( Skewness ) в табл. 6.16 положителен, можно прийти к выводу, что в распределении остатков, полученных по стационарной модели, наблюдается положительная асимметрия. Отсюда можно сделать вывод, что в динамике курса доллара к рублю чаще наблюдались резкие (вполне очевидно, что незначительные плавные колебания курса легко поддаются прогнозированию) подъемы, чем аналогичные падения. В свою очередь величина коэффициент эксцесса ( Kurtosis ) существенно выше 3, что свидетельствует об «островершинном» распределении остатков. По сути, это означает, что в этом распределении имеется ярко выраженное ядро плотности распределения, внутри которого диапазон колебаний величины остатков незначителен, и рассеянное «гало», где разброс колебаний величины остатков весьма значителен. Поскольку величина тестовой статистики Жарка — Бера составила 11990,08, а уровень ее значимости (Probability) оказался равен нулю, то, следовательно, мы вынуждены отвергнуть гипотезу о нормальном распределении остатков. Поскольку, как мы уже говорили нашим читателям, при уровне значимости критерия Жарка — Бера (Probability) меньше 0,05 нулевая гипотеза о нормальном распределении отклоняется.