Владимир Брюков - Как предсказать курс доллара. Эффективные методы прогнозирования с использованием Excel и EViews

log(USDollar) с log(USDollar(-l)) МА(1), (6.8)

где с — константа;

log(USDollar(-l)) — логарифм от переменной с лагом в один месяц;

МА(1) — представляет собой скользящую среднюю первого порядка.

При этом следует иметь в виду одну тонкость: в опциях диалогового мини-окна EQUATION ESTIMATION (оценка уравнения) по умолчанию устанавливается параметр BACKCAST МА TERMS (рекурсивное вычисление предыдущей ошибки в МА-процессе). В этом случае значение предыдущей ошибки (отклонения прогноза от фактического курса доллара в прошлом месяце) для точечного прогноза по первому наблюдению находится рекурсивным методом (см. ввод этой опции на рис. 6.5).

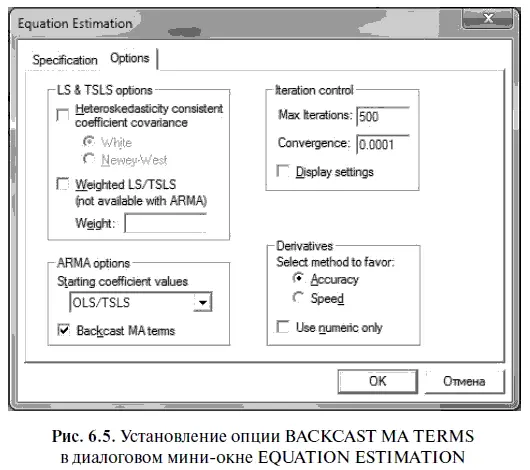
Если в параметре BACKCAST МА TERMS убрать «галочку», значение прошлой ошибки в точечном прогнозе для первого наблюдения приравнивается нулю, поскольку оно на тот момент отсутствует. В свою очередь в случае применения в статистической модели скользящей средней второго порядка прошлые ошибки при прогнозировании не только первого, но и второго наблюдений либо приравниваются нулю, либо вычисляются рекурсивным методом.

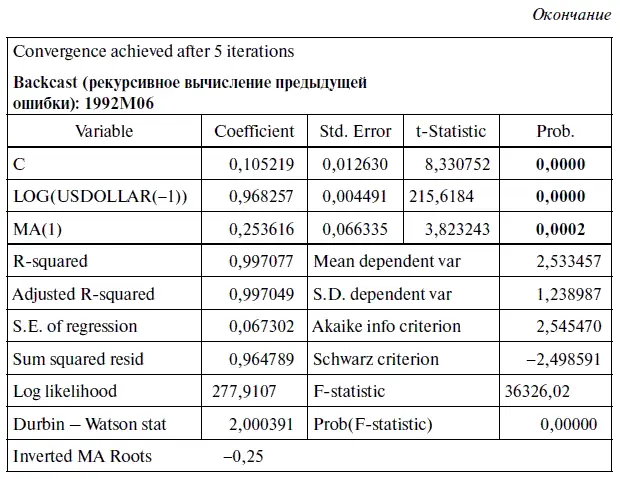
В результате ввода в диалоговое мини-окно EQUATION ESTIMATION формулы (6.7) получается следующий вывод данных (табл. 6.6). Причем все полученные коэффициенты в этом уравнении у нас получились статистически значимыми (все выделенные жирным шрифтом значения Prob. меньше 0,05). Кстати, в таблице появляется информация о рекурсивном вычислении предыдущей ошибки относительно июня 1992 г. — Backcast: 1992М06. После замены буквенных обозначений вычисленными коэффициентами получилось следующее уравнение регрессии со скользящей средней:

log(USDollar) = 0,105219 + 0,968257 × log(USDollar(-l)) + 0,253616 e t- 1, (6.9)

где е t- 1— прошлая ошибка (отклонение фактического курса доллара от его прогноза), которая в уравнении (6.8) представлена скользящей средней МА(1).

К сожалению, в отличие от формулы (6.5) формулу (6.9) нельзя путем потенцирования привести к исходному временному ряду, что обусловлено применением в этой статистической модели скользящей средней, рассчитанной применительно к остаткам, полученным от логарифмического ряда. Поэтому интерпретация формулы (6.9) будет достаточно затруднительной, поскольку мы вынуждены ее дать относительно логарифмического, а не исходного временного ряда.

Тем не менее все-таки эту интерпретацию нужно представить, чтобы смысл уравнения (6.9) был для читателя более понятен. Во-первых, рост на одну единицу логарифмического значения курса доллара в текущем месяце в среднем способствовал повышению логарифмического значения курса доллара в прогнозируемом месяце на 0,968 ед. (при исходном уровне логарифмического значения курса доллара, равном 0,105 ед.). Во-вторых, рост на одну единицу отклонения логарифмического значения фактического курса доллара от его прогноза способствовал повышению логарифмического значения курса доллара в прогнозируемом месяце в среднем на 0,254 ед.

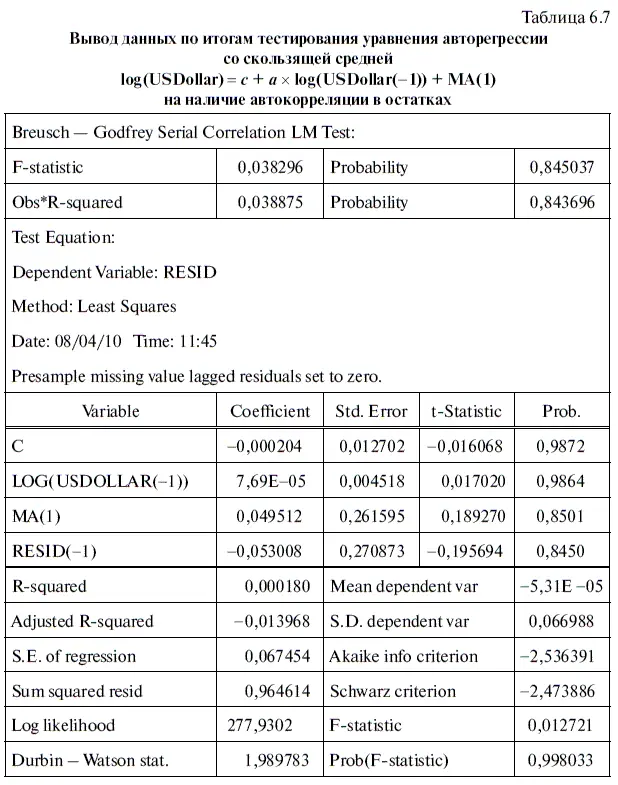
Теперь посмотрим, есть ли автокорреляция в остатках у полученной статистической модели, а потому вновь проведем тестирование с помощью LM -теста Бройша — Годфри. Причем при выполнении теста в диалоговом мини-окне LAG SPECIFICATION (лаговая спецификация) нужно, как и в предыдущем случае, установить 1, поскольку в нашем уравнении авторегрессии со скользящим средним ARMA(1,1) как факторная переменная, так и скользящая средняя имеют один лаг (см. формулу (6.8)).

По результатам проведения этого теста у нас получилась табл. 6.7, данные которой уверенно свидетельствуют об отсутствии автокорреляции в остатках. Такой вывод можно сделать исходя из того, что уровень значимости как основного критерия теста Obs × R-squared (Наблюдения × R 2), так и дополнительного — F-statistic ( F -критерия) существенно выше 0,05.

Теперь протестируем ARMA-структуру этого уравнения на стационарность, воспользовавшись при этом алгоритмом действий № 13. В результате у нас получится табл. 6.8, свидетельствующая, что ARMA-структура этой статистической модели получилась стационарной, поскольку все обратные корни в этом уравнении лежат внутри единичного круга. Этот вывод можно найти в нижней части этой таблицы.