Владимир Брюков - Как предсказать курс доллара. Эффективные методы прогнозирования с использованием Excel и EViews

Таким образом, с помощью метода, предложенного американским экономистом Д. Гуйарати, нам удалось выяснить, что во временн о м ряде по ежемесячному курсу доллара, охватывающем период с июня 1992 г. по апрель 2010 г., после августовского дефолта 1998 г. произошли следующие структурные изменения: во-первых, в августе 1998 г. произошел структурный сдвиг; во-вторых, в сентябре 1998 г. имело место первое структурное изменение наклона (изменился коэффициент регрессии факторной переменной с лагом в два месяца); в-третьих, в октябре 1998 г. имело место второе структурное изменение наклона (изменился коэффициент факторной переменной с лагом один месяц).

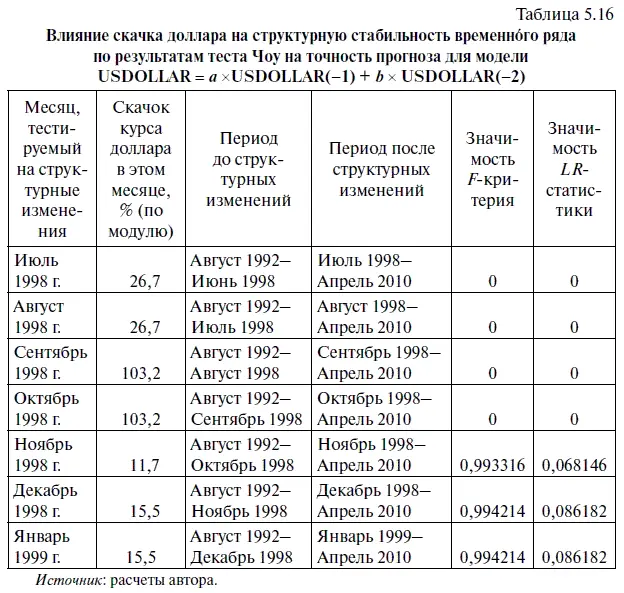
А теперь посмотрим, подтвердит ли эти структурные изменения во временном ряде тест Чоу на точность прогноза. С этой целью проведем тестирование модели USDOLLAR = а × USDOLLAR(-l) + b × USDOLLAR(-2), построенной на основе данных за период с июня 1992 г. по апрель 2010 г. При этом проверять на наличие структурной стабильности будем такие месяцы, как июль — декабрь 1998 г. и январь 1999 г., поскольку тест Д. Гуйарати показал наличие структурных изменений в августе — октябре 1998 г., но для большей надежности мы решили несколько расширить этот временн о й диапазон.

В результате получилась табл. 5.16, согласно которой уровень значимости F -критерия и LR -статистики для июля — октября 1998 г. оказался равен нулю, что опровергает нулевую гипотезу о структурной стабильности временного ряда относительно тестируемых наблюдений. Кстати, на основе этого теста аналогичный вывод можно сделать и для всех наблюдений с августа 1992 г. по октябрь 1998 г. включительно; в то время как уровень значимости F -критерия и LR -статистики по итогам проведения теста Чоу на точность прогноза относительно ноября 1998 г. и остальных, более поздних наблюдений (за исключением января — февраля 2009 г., но этот факт мы рассматриваем как временное явление) будет выше 0,05. Отсюда можно сделать вывод, что нулевая гипотеза о наличии структурной стабильности в этой части временного ряда подтверждается, что совпадает с аналогичными результатами, полученными с помощью метода Д. Гуйарати.

Чтобы построить статистическую модель с приемлемым диапазоном интервального прогноза, попробуем — с учетом итогов теста Чоу на точность прогноза — исключить из расчетной базы данных период с июля 1992 г. по октябрь 1998 г. (включительно). После чего на основе рыночных данных с ноября 1998 г. по апрель 2010 г. с помощью модели USDOLLAR =а × USDOLLAR(-l) + b × USDOLLAR(-2) построим новое уравнение регрессии, вывод итогов которого представлен в табл. 5.17. Как нетрудно заметить, все переменные, включенные в это уравнение регрессии, оказались статистически значимыми (Prob. = 0). Далее эту модель будем называть нестационарной моделью с оптимизированным временным рядом, чтобы отличить ее от модели с полным временным рядом.

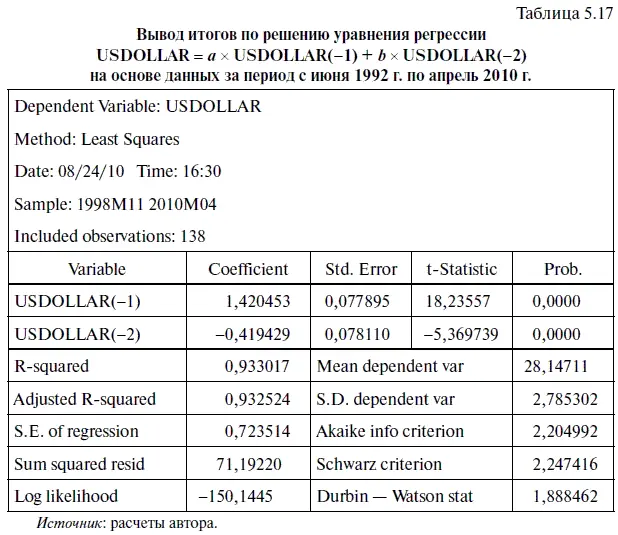
В результате точечный прогноз по курсу доллара на май 2010 г. оказался равен 29,287 руб. Таким образом, последняя цифра лишь немного отклонилась от 29,3137 руб., т. е. от точечного прогноза на май 2010 г., составленного по статистической модели с полным временным рядом (на основе данных с июня 1992 г. по апрель 2010 г.).

Далее составим точечные и интервальные прогнозы как для всех предыдущих наблюдений, включенных в базу данных, начиная с ноября 1998 г., так и на май 2010 г. (это наблюдение в базу данных не вошло). При этом будем пользоваться алгоритмом действий № 11 «Как в EViews построить точечный прогноз» и алгоритмом действий № 12 «Как в EViews построить интервальные прогнозы».

В результате появилась возможность сопоставить заданные уровни надежности с фактической долей точных интервальных прогнозов. После проведения соответствующих подсчетов получилась табл. 5.18. Судя по этой таблице, доля точных прогнозов у предложенной модели оказалась незначительно ниже заданного уровня при 99,9 %-ном и 99 %-ном уровнях надежности. В то время как при 95 %-ном уровне надежности и ниже доля точных интервальных прогнозов становится на 0,7 процентного пункта выше заданного уровня. По мере снижения заданного уровня надежности эта положительная разница растет, достигая максимума при 40 %-ном уровне надежности, когда она равна 31,2 процентного пункта.