Владимир Брюков - Как предсказать курс доллара. Эффективные методы прогнозирования с использованием Excel и EViews

USDOLLAR = 1,927 × USDOLLAR(-1) — 0,928 × USDOLLAR(-2) (5.9.1)

При этом интерпретация уравнения (5.9.1) была следующая: во-первых, рост на 1 руб. курса доллара в текущем месяце способствовал повышению курса доллара в будущем месяце в среднем на 1,927 руб.; во-вторых, рост на 1 руб. курса доллара в прошлом месяце способствовал снижению курса доллара в будущем месяце в среднем на -0,928 руб.

В августе 1998 г., когда произошел структурный сдвиг, формула тренда приобрела иной вид:

USDOLLAR = 1,927 × USDOLLAR(-1) — 0,928 × USDOLLAR(-2) + 1,865 × DUMMY (5.9.2)

Интерпретация формулы (5.9.2) аналогична предыдущей, за исключением того, что появление в уравнении фиктивной переменной DUMMY свидетельствует о единовременном повышении курса доллара в августе 1998 г. на 1,865 руб.

В сентябре 1998 г., когда имело место первое структурное изменение наклона, формула тренда снова изменилась:

USDOLLAR = 1,927 × USDOLLAR(-1) — 0,928 × USDOLLAR(-2) + 0,754 × USDOLLAR(-2) × DUMMY09 + 1,865 × DUMMY

(5.9.3)

Формула (5.9.3) отличается от уравнения (5.9.2) тем, что у нее появилась фиктивная переменная наклона USDOLLAR(-2) × DUMMY09, показывающая увеличение коэффициента регрессии у переменной

USDOLLAR(-2) на 0,754. Следовательно, с этого месяца вклад переменной USDOLLAR(-2) в динамику курса доллара с учетом структурного наклона, стал следующим: рост на 1 руб. курса доллара в прошлом месяце способствовал снижению курса доллара в будущем месяце в среднем на -0,174 руб.

В октябре 1998 г. после второго структурного изменения наклона наша формула приобрела следующий вид:

USDOLLAR = 1,927 × USDOLLAR(-1) — 0,818 × USDOLLAR(-1) × DUMMY10- 0,928 USDOLLAR(-2) + 0,754 × USDOLLAR(-2) × DUMMY09 + 1,865 × DUMMY

(5.9.4)

Формула (5.9.4) отличается от предыдущей лишь тем, что у нее появилась фиктивная переменная наклона USDOLLAR(-1) × DUMMY10, которая показывает уменьшение коэффициента регрессии у переменной USDOLLAR(-1) на -0,818. Следовательно, с октября 1998 г. вклад переменной USDOLLAR(-2) в динамику курса доллара изменился таким образом: рост на 1 руб. курса доллара в текущем месяце способствовал повышению курса доллара в будущем месяце в среднем на 1,109 руб.

Следует иметь в виду, что формула (5.9.4) отличается, например, от формулы (3.4), описывающей аналогичный период, поскольку у этих формул разное число оцениваемых параметров.

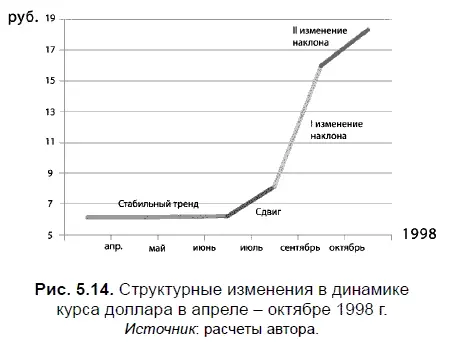
На диаграмме, представленной на рис. 5.14, изображен график, наглядно показывающий характер структурных изменений в динамике курса доллара, произошедших во время кризиса 1998 г. В частности, здесь можно увидеть как структурный сдвиг, произошедший в августе 1998 г., так и первое, и второе структурные изменения наклона, имевшие место в сентябре и октябре 1998 г.

Американский экономист Д. Гуйарати для оценки структурных изменений в динамике тренда, происходящих в момент времени t*, предложил оценивать параметры следующего уравнения регрессии с фиктивными переменными:

Y t = а + b × Z t+ с × t + d × (Z t× t) + е, (5.10)

где Y t— зависимая переменная; t — время;

а, b, с, d — параметры уравнения регрессии;

е — ошибка (остатки);

Z t— фиктивная переменная, которая при t < t' равна нулю, а при t ≥ t' равна единице.

Следовательно для момента времени t < t' мы получим следующее уравнение регрессии:

Z t= 0 => Y,= а + b × 0 + с × t + d × (0 × t) + e=>Y t= a+ c × t + e. (5.10.1)

Соответственно для момента времени t> f уравнение примет такой вид:

Z t= 1 => Y t= a+b × l+c × t + d × (1 × t ) + е =>

=> Y t= (a+b) + (c+d) × t + e. (5.10.2)

Сравнив уравнение (5.10.1) с уравнением (5.10.2), нетрудно прийти к выводу, что при Z t= 1 свободный член уравнения а 2 =(а+ b), а коэффициент регрессии — c 2 × t = (c+d) × t. Соответственно при Z t= 0 свободный член уравнения а 1 = а, а коэффициент регрессии — с 1 × t= с × t. Таким образом, параметр b можно рассматривать как разницу между а 1и а 2, т. е. между свободными членами уравнений (5.10.1) и (5.10.2). В свою очередь параметр d следует рассматривать как разницу между c 1и с 2, т. е. между коэффициентами регрессии уравнений (5.10.1) и (5.10.2). Следовательно, параметр b оценивает структурный сдвиг, а параметр d — структурное изменение наклона в уравнении регрессии, произошедшее в момент времени t' . Оценку параметров bud можно провести, решив уравнение регрессии, а затем оценив их значимость при помощи t- критерия Стьюдента.

Подробности по этой теме можно узнать, ознакомившись с соответствующей литературой [17] См., например: Эконометрика. С. 327–334. .