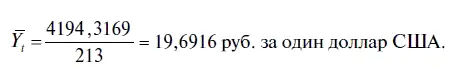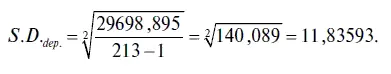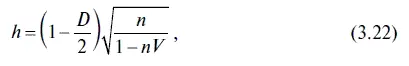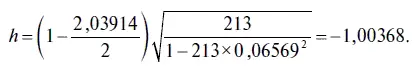Владимир Брюков - Как предсказать курс доллара. Эффективные методы прогнозирования с использованием Excel и EViews

3. Следующий параметр уравнения регрессии, на наш взгляд, не представляет каких-либо трудностей для его понимания — MEAN DEPENDENT VAR (СРЕДНЕЕ ЗНАЧЕНИЕ ЗАВИСИМОЙ ПЕРЕМЕННОЙ). При этом среднее значение зависимой переменной рассчитывается по довольно простой формуле

где п — количество наблюдений;

Y t— зависимая переменная, ежемесячный курс доллара.

В нашем случае среднее значение (вернее сказать, среднее хронологическое, поскольку мы берем период за 213 месяцев) зависимой переменной будет равно

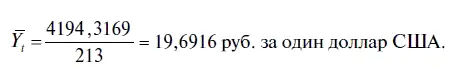
4. Еще один показатель, характеризующий зависимую переменную данного уравнения регрессии — S.D. DEPENDENT VAR (СТАНДАРТНОЕ ОТКЛОНЕНИЕ ЗАВИСИМОЙ ПЕРЕМЕННОЙ). При этом стандартное отклонение зависимой переменной находится следующим образом:

В нашем случае стандартное отклонение зависимой переменной вычисляется достаточно легко:

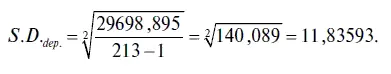
5. Важными параметрами уравнения регрессии являются два информационных критерия — AKAIKE INFO CRITERION (ИНФОРМАЦИОННЫЙ КРИТЕРИЙ АКАИКА) и SCHWARZ CRITERION (КРИТЕРИЙ ШВАРЦА). Оба этих информационных критерия можно использовать в качестве критериев для определения в уравнении регрессии оптимальной длины лага. При этом они основаны на принципе снижения остаточной суммы квадратов при добавлении значимого фактора. Так, информационный критерий Акаика находится по следующей формуле:

AIC = -2LL: T + 2k: T, (3/20)

где LL — логарифм максимального правдоподобия;

T — количество наблюдений;

k — общее количество лагов в уравнении авторегрессии.

В нашем случае информационный критерий Акаика равен

AIC = -2×256,1815: 213 × 2 × 3: 213 =2,4336.

В свою очередь информационный критерий Шварца рассчитывается по формуле

SC = -2LL: T + (k ln T):T. (3.21)

Относительно нашего уравнения регрессии информационный критерий Шварца имеет следующее значение:

SC = -2 × 256,1815: 213 + (3ln213):213 =2,4809.

Обычно оцениваемая статистическая модель лучше соответствует фактическим данным при более высоком порядке р и q в модели ARMA(/? q). Платой за это кажущееся повышение точности является вполне очевидная потеря в простоте статистической модели и в экономии включенных в него параметров, поэтому для достижения компромисса между точностью уравнения регрессии и экономией его параметров пользуются информационными критериями Акаика и Шварца.

При выборе из двух уравнений регрессии обычно предпочтение отдается той статистической модели, у которой меньше значения этих информационных критериев. Следует также заметить, что информационный критерий Шварца по сравнению с критерием Акаика позволяет отбирать уравнения регрессии с более экономичными параметрами.

Как мы уже говорили, в уравнениях авторегрессии при тестировании остатков на наличие автокорреляции критерий Дарбина — Уотсона теряет свою мощность, и в этих случаях приходится пользоваться иными критериями. Например, тем, кто работает в Excel, с этой целью проще воспользоваться критерием h Дарбина, или, как его еще называют, h -статистикой Дарбина. Его расчет выполняется по следующей формуле:

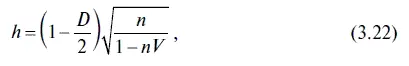
где D — критерий Дарбина — Уотсона;

п — количество наблюдений;

V — квадрат стандартной ошибки при лаговой факторной переменной Y t_ 1.

Например, в нашем случае критерий h Дарбина имеет следующую величину:

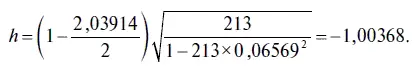
При увеличении объема выборки распределение h -статистики стремится к нормальному с нулевым математическим ожиданием и дисперсией, равной 1. Поэтому гипотеза об отсутствии автокорреляции в остатках отвергается, если фактическое значение h -статистики оказывается больше, чем критическое значение нормального распределения. Для проверки по критерию h Дарбина гипотезы о наличии автокорреляции в остатках проще воспользоваться следующим правилом.