Владимир Брюков - Как предсказать курс доллара. Эффективные методы прогнозирования с использованием Excel и EViews

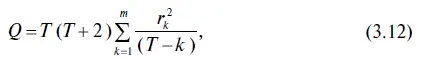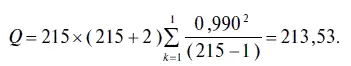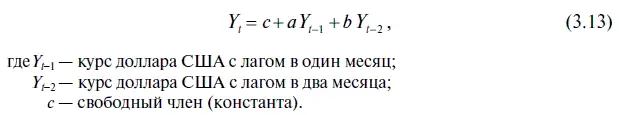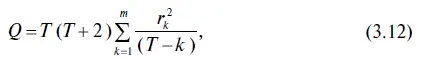
где Т — число наблюдений;

r k— автокорреляция k- го порядка;

m — число проверяемых лагов.

Например, для лага 1-го порядка формула (3.12) имеет следующее значение:

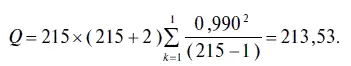
Следует иметь в виду, что в том случае, когда в табл. 3.1 значимость (Prob.) 0-статистики будет больше 0,05, то нулевую гипотезу об отсутствии автокорреляции между уровнями ряда с лагом А:-го порядка нельзя считать опровергнутой с 95 %-ным уровнем надежности. Если значимость 0-статистики будет больше 0,01, но меньше 0,05, то нулевую гипотезу об отсутствии автокорреляции между уровнями ряда с лагом А:-го порядка нельзя считать опровергнутой с 99 %-ным уровнем надежности. Судя по коррелограмме исходных уровней временного ряда USDollar (см. табл. 3.1), значимость Q-статистики для всех 36 лагов равна нулю, поэтому нулевая гипотеза об отсутствии автокорреляции в остатках отклоняется для всех лагов.

После того как с помощью соответствующей коррелограммы (см. табл. 3.1) мы пришли к выводу, что для получения оптимального прогноза по курсу доллара следует построить модель авторегрессии 2-го порядка AR(2), следующим нашим шагом должно стать нахождение ее параметров. Правда, для этого развернутое уравнение авторегрессии AR(2), представленное в формуле (3.10), необходимо немного упростить. С этой целью из формулы следует убрать остатки, которые появятся только после решения этого уравнения. Кроме того, чтобы убрать у коэффициентов факторных переменных подстрочные индексы (цифры), обозначим их различными буквами. В результате формула (3.10) приобретет более удобный для решения вид:

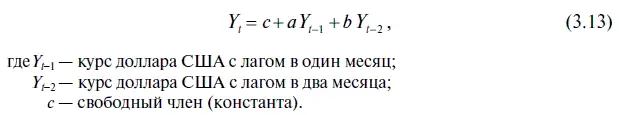
Мы уже научились решать уравнения регрессии в Excel (см. алгоритм действий № 3 «Как решить уравнение регрессии в Excel»), поэтому, используя этот алгоритм, можно получить соответствующее уравнение авторегрессии, которое, как известно, является частным случаем уравнения регрессии и отличается от последнего лишь наличием лаговых факторных переменных. А для загрузки и первичной обработки данных по ежемесячному курсу доллара необходимо воспользоваться алгоритмом действий № 1 «Как строить диаграммы в Microsoft Excel» — Шаг 1 «Поиск данных, их загрузка и первичная обработка в Excel».

Далее создадим в Excel три столбца: во-первых, с зависимой переменной USDollar — ежемесячный курс доллара США; во-вторых, с двумя независимыми переменными USDollar(-l) — курс доллара США с лагом в один месяц и USDollar(-2) — курс доллара США с лагом в два месяца. При этом загруженная база данных по американской валюте охватывает период с июня 1992 г. по апрель 2010 г.

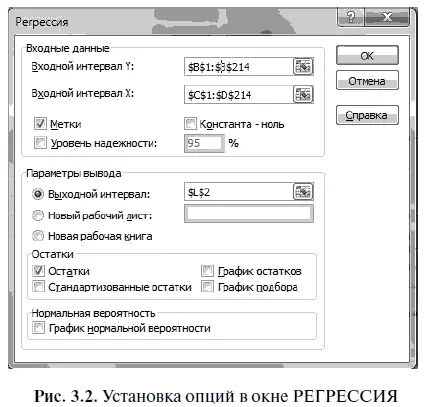
Далее, согласно алгоритму действий № 3 «Как решить уравнение регрессии в Excel», установим в появившемся окне РЕГРЕССИЯ следующие опции (рис. 3.2): ВХОДНОЙ ИНТЕРВАЛ Y ($В$1:$В$214); ВХОДНОЙ ИНТЕРВАЛ X ($C$1:$D$214); УРОВЕНЬ НАДЕЖНОСТИ (99); ВЫХОДНОЙ ИНТЕРВАЛ ($L$2).

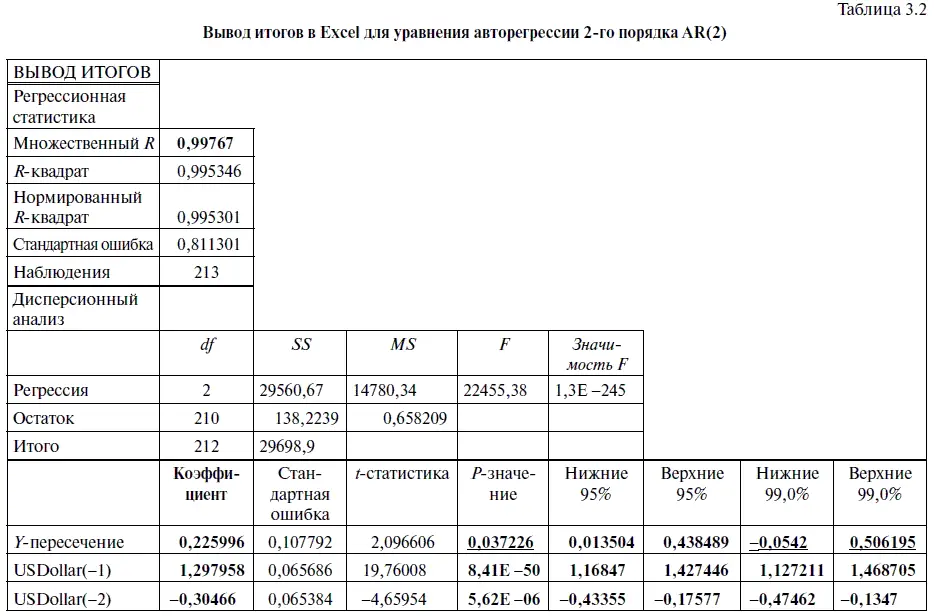
В результате решения в Excel уравнения авторегрессии AR(2) со свободным членом мы получим следующий ВЫВОД ИТОГОВ, представленный в виде табл. 3.2. Возьмем из этой таблицы значения коэффициентов (см. столбец «Коэффициенты») и, подставив их в формулу (3.13), получим следующее уравнение авторегрессии (с округлением):

USDollar = 0,2260 + 1,2980 USDollar(-l) — 0,3047 USDollar(-2),

где USDollar — зависимая переменная, курс доллара США;

USDollar(-l) — независимая переменная, курс доллара США с лагом в один месяц;

USDollar(-2) — независимая переменная, курс доллара США с лагом в два месяца;

0,2260 — свободный член (константа).

При этом экономическая интерпретация этого уравнения авторегрессии 2-го порядка следующая: во-первых, в период с июня 1992 г. по апрель 2010 г. при исходном уровне 0,2260 руб. рост на 1 руб. курса доллара в текущем месяце приводил к повышению прогнозируемого курса доллара в будущем месяце в среднем на 1,2980 руб.; во-вторых, одновременно с этим рост курса доллара в прошлом месяце приводил к снижению прогнозируемого курса доллара в будущем месяце в среднем на 0,3047 руб.