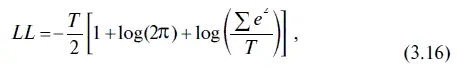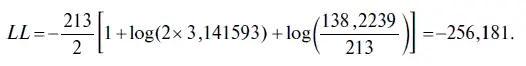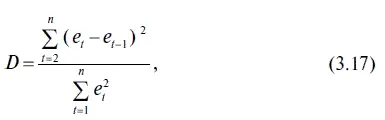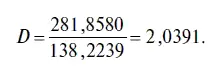Владимир Брюков - Как предсказать курс доллара. Эффективные методы прогнозирования с использованием Excel и EViews

Если вспомнить, что формула (3.14) фактически означает уравнение авторегрессии 2-го порядка со свободным членом, то миниокно EQUATION SPECIFICATION можно заполнить другой, более краткой, но вполне равнозначной формулой:

USDollar AR(1) AR(2) с, (3.15)

где USDollar — зависимая переменная;

AR(1) — авторегрессия 1-го порядка, или USDollar(-l);

AR(2) — авторегрессия 2-го порядка, или USDollar(-2).

Итак, все опции, необходимые для решения уравнения авторегрессии, установлены. Далее щелкаем кнопку ОК в окне EQUATION ESTIMATION. В результате чего получаем данные с параметрами уравнения авторегрессии, которые мы поместили в табл. 3.3. При этом не стоит удивляться тому, что после соответствующей корректировки количество наблюдений у нас сократилось с 215 до 213. Это обусловлено тем, что при создании факторных переменных с лагом в один и в два месяца мы потеряли два наблюдения. В результате теперь наша скорректированная выборка охватывает период не с июня 1992 г., а с августа 1992 г. по апрель 2010 г.

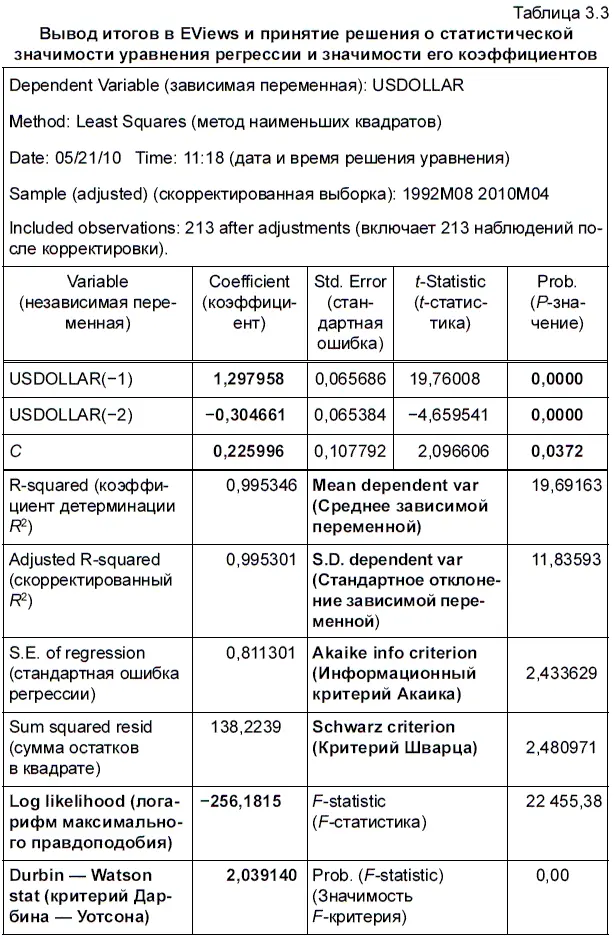
Чтобы нашему читателю было легче понять содержащиеся в табл. 3.3 англоязычные термины, они даются вместе с параллельным переводом в скобках. Если сравнить табл. 3.3 с выводом итогов, полученным после решения этого же уравнения авторегрессии в Excel (см. табл. 3.2), то можно прийти к выводу о тождественности большей части информации, имеющейся в обеих таблицах. Следует также заметить, что как в программе Excel, так и в EViews мы смогли получить коэффициенты уравнения регрессии с одинаковым уровнем точности.

Какой статистический смысл имеют те или иные параметры уравнения регрессии при выводе итогов в Excel, уже говорилось в главе 1 книги. Однако при выводе итогов в EViews мы получаем новую информацию о других важных параметрах уравнения регрессии, которых нет при выводе итогов в Excel. Чтобы обратить внимание читателя на эти дополнительные параметры, мы выделили их жирным шрифтом в табл. 3.3. Познакомимся со статистическим смыслом этих еще не изученных нами дополнительных параметров уравнения регрессии.

1. В таблице 3.3 среди пока неизвестных нам параметров уравнения регрессии можно назвать такой важный показатель, как LOG LIKELIHOOD (ЛОГАРИФМ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ), который используется в качестве критерия для отбора наиболее адекватных уравнений регрессии. Чем выше логарифм максимального правдоподобия, тем более адекватным считается уравнение регрессии. При этом логарифм максимального правдоподобия находится по следующей формуле:

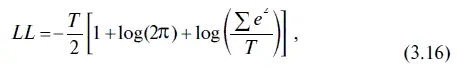
где Т — количество наблюдений;

е — отклонение (остатки) прогноза от фактического курса доллара;

π — число пи, равное 3,141593…

В нашем случае логарифм максимального правдоподобия имеет следующее значение:

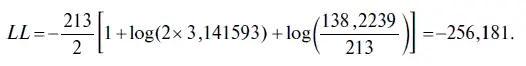
2. Следующим еще не изученным нами параметром уравнения регрессии является DURBIN-WATSON STAT (КРИТЕРИЙ ДАРЬИНА — УОТСОНА), который является тестом на наличие автокорреляции в остатках. Как мы уже говорили, при наличии автокорреляции в остатках оценки коэффициентов уравнения регрессии нельзя назвать состоятельными и эффективными. При этом критерий Дарбина — Уотсона находится следующим образом:

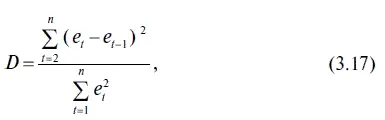
где п — количество наблюдений;

е t— отклонение (остатки) прогноза от фактического курса доллара;

е t −1 — отклонение (остатки) прогноза от фактического курса доллара с лагом в один месяц.

В нашем случае критерий Дарбина — Уотсона имеет следующее значение:

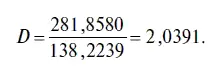
Правда, критерий Дарбина — Уотсона нельзя использовать для тестирования уравнений авторегресии на наличие автокорреляции в остатках, поскольку в этом случае он теряет свою мощность. Это объясняется тем, что применение критерия Дарбина — Уотсона предполагает строгое соблюдение предпосылки о разделении переменных на зависимую (результативную) и независимую (факторную) переменную. В уравнениях авторегрессии, как известно, в правой части уравнения имеются лаговые значения результативной переменной, а следовательно, указанная предпосылка не соблюдается. В этом случае фактическое значение критерия Дарбина — Уотсона приблизительно равно 2 как при наличии, так и при отсутствии автокорреляции в остатках. Тем не менее в обычных уравнениях регрессии этот критерий весьма полезен для тестирования остатков на наличие автокорреляции.