Денис Соломатин - Математические модели в естественнонаучном образовании. Том II

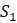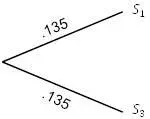
По приведенной выше таблицы данных выберем два ближайших таксона, и 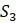. Поскольку они находятся на расстоянии 0,27 друг от друга, изобразим на рисунке 5.6 каждое ребро с длиной .

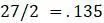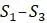Рисунок 5.6. UPGMA; шаг 1.

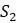Затем объединяем и в группу и усредняем расстояния и до каждого отдельного таксона, чтобы получить расстояние от группы до этого таксона. Например, расстояние между группой и равно 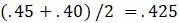, а расстояние между 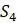и равно 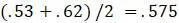. Таким образом, исходная таблица сводится к таблице 5.3.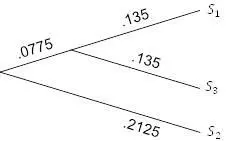

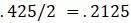Таблица 5.3. Расстояния между групп; UPGMA, Шаг 1

.425 .575

.50

Теперь просто повторяем процесс, используя расстояния в таблице 5.3. Поскольку ближайшими таксонами и/или группами в новой таблице являются и , которые находятся на расстоянии 0,425 друг от друга, то получаем рисунок 5.7.

Рисунок 5.7. UPGMA; шаг 2.

Ребро должно иметь длину , в то время как другое новое ребро должно иметь длину 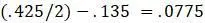, потому что уже есть ребро длины 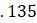для учета некоторого расстояния между и другими таксонами.

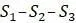Снова объединив таксоны, формируем группу и вычисляем расстояние от неё до 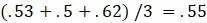путем усреднения исходных расстояний от до каждого из , и . Это приводит к значению . Обратите внимание, что это не то же самое, что усреднение расстояния от 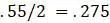до и до . Поскольку новая таблица расстояний будет иметь это значение в качестве единственной записи, нет необходимости приводить ее. Изобразим рисунок 5.8, считая, что расстояние от корня до равно . Конечное ребро имеет длину. 0625, таким образом, помещаем оставшийся таксон на расстоянии 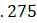от корня.